Aufgabe:
Es sei \( \boldsymbol{a} \in \mathbb{R}^{n} \). Prüfen sie mithilfe des Untervektorraumkriteriums, ob die folgenden Mengen (mit der üblichen Addition und Multiplikation mit einem Skalar) jeweils einen Vektorraum über \( \mathbb{R} \) bilden.
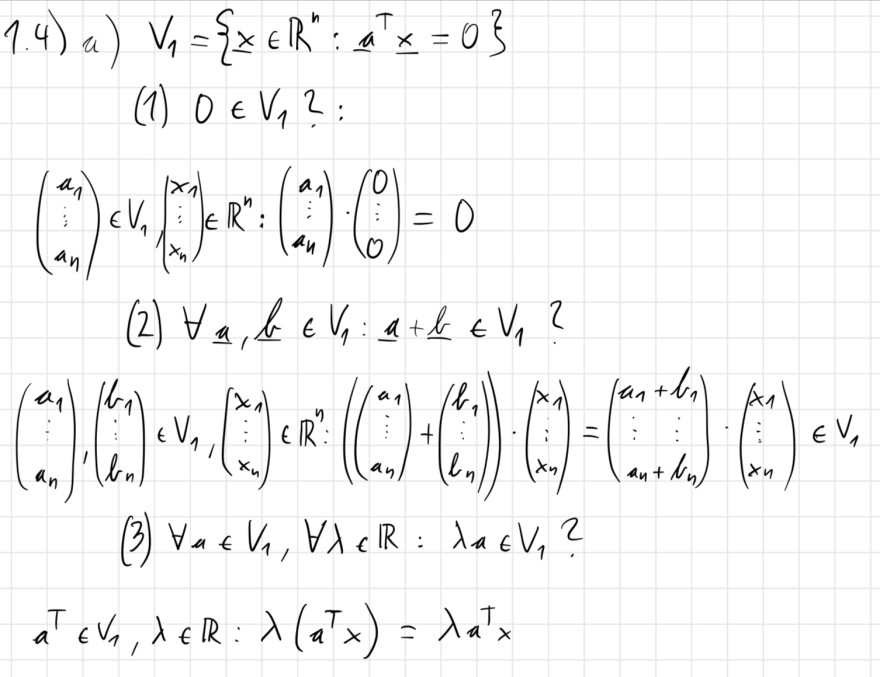
Ist das so korrekt? Ich bin mir unsicher, ob ich die Aufgabe so richtig verstanden habe.