Ich soll von dieser allgmeinen (n x n)-Matrix, wobei n jede natürliche Zahl sein kann, die Determinante berechnen bzw. bestimmen. Kann mir jemand helfen, da ich nicht weiss, wie ich das tun soll.
Text erkannt:
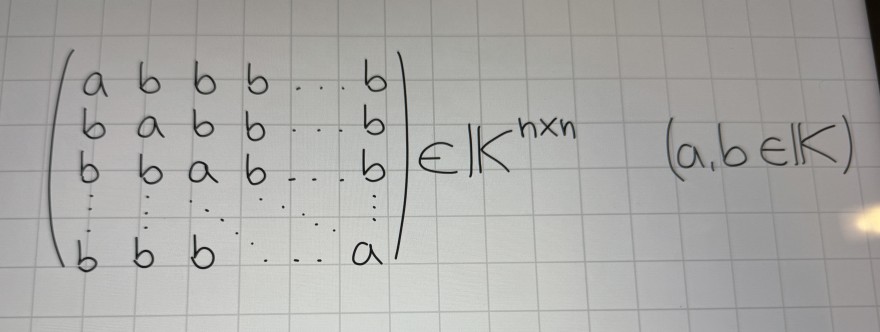
\( \left(\begin{array}{cccccc}a & b & b & b & \cdots & b \\ b & a & b & b & \cdots & b \\ b & b & a & b & \cdots & b \\ \vdots & \vdots & \ddots & \cdots & \vdots \\ b & b & b & \cdots & \cdots & a\end{array}\right) \in \mathbb{K}^{n \times n} \quad(a, b \in \mathbb{K}) \)