Übergangsmatrix beim Carsharing

Question

Aufgabe:

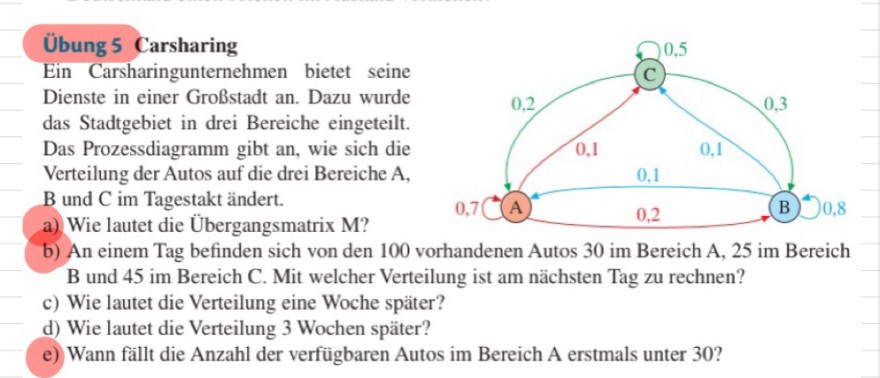
Ein Carsharingunternehmen bietet seine Dienste in einer Großstadt an. Dazu wurde das Stadtgebiet in drei Bereiche eingeteilt. Das Prozessdiagramm gibt an, wie sich die Verteilung der Autos auf die drei Bereiche $\mathrm{A}$, $\mathrm{B}$ und $\mathrm{C}$ im Tagestakt ändert.

a) Wie lautet die Übergangsmatrix M?

b) An einem Tag befinden sich von den 100 vorhandenen Autos 30 im Bereich A, 25 im Bereich B und $45 \mathrm{im}$ Bereich C. Mit welcher Verteilung ist am nächsten Tag zu rechnen?

c) Wie lautet die Verteilung eine Woche später?

d) Wie lautet die Verteilung 3 Wochen später?

e) Wann fällt die Anzahl der verfügbaren Autos im Bereich A erstmals unter 30 ?

Problem/Ansatz:

Komme bei e) nicht weiter. Kann jemand helfen

Answer 1

Berechne

        $M^n \cdot \begin{pmatrix}30\\25\\45\end{pmatrix}$

für jedes $n$ von 1 bis 7.

Answer 2

a)

$$M = \begin{pmatrix} 0.7 & 0.1 & 0.2 \\ 0.2 & 0.8 & 0.3 \\ 0.1 & 0.1 & 0.5 \end{pmatrix}$$

b)

$$v_1 = M \cdot \begin{pmatrix} 30\\25\\45 \end{pmatrix}$$

c)

Rechne die Verteilung für ein paar weitere Tage aus. Es dauert weniger als eine Woche.