Aufgabe:
…Hallo,
Für Aufgabe 2 und 3 sind meine Lösungen hochgeladen. Der Tutor meinte nun, dass man angeben soll welche spezielle Eigenschaft der Funktion hier verwendet wird. Kann mir jemand da helfen? Würde mich riesig freuen
Text erkannt:
2. Aufgabe: Bilder des Einheitskreises
Beschreiben oder zeichnen Sie das Bild (wo wohldefiniert) des Einheitskreises
\( \mathbb{S}=\{z \in \mathbb{C}|| z \mid=1\} \)
unter der folgenden Abbildungen:
a) \( f(z)=\frac{1}{z} \)
b) \( g(z)=\frac{1}{z-1} \)
c) \( h(z)=\frac{1}{z-2} \)
3. Aufgabe: Konforme Abbildungen
Sei \( H S=\{z \in \mathbb{C}|| z \mid<1, \operatorname{Im}(z)>0\} \) die obene Halbkreisscheibe.
a) Beschreiben oder zeichnen Sie das Bild von \( H S \) unter der Abbildung \( f(z)=\frac{1}{z+1} \).
b) Bestimmen Sie eine konforme Abbildung, die \( H S \) auf \( K_{1}=\{z \in \mathbb{C} \mid \operatorname{Im}(z)<0, \operatorname{Re}(z)>0\} \) abbildet.
c) Bestimmen Sie eine konforme Abbildung, die \( H S \) auf \( K_{2}=\{z \in \mathbb{C} \mid \operatorname{Im}(z)>0, \operatorname{Re}(z)>0\} \) abbildet.
d) Bestimmen Sie eine konforme Abbildung, die \( H S \) auf \( H=\{z \in \mathbb{C} \mid \operatorname{Im}(z)>0\} \) abbildet.
Text erkannt:
23:00
HA 6 (5).pdf - Schreibgeschützt
\( \Leftarrow \)
[8
\( \uparrow \)
O
\( \kappa \nearrow \)
\( K \searrow \)
0
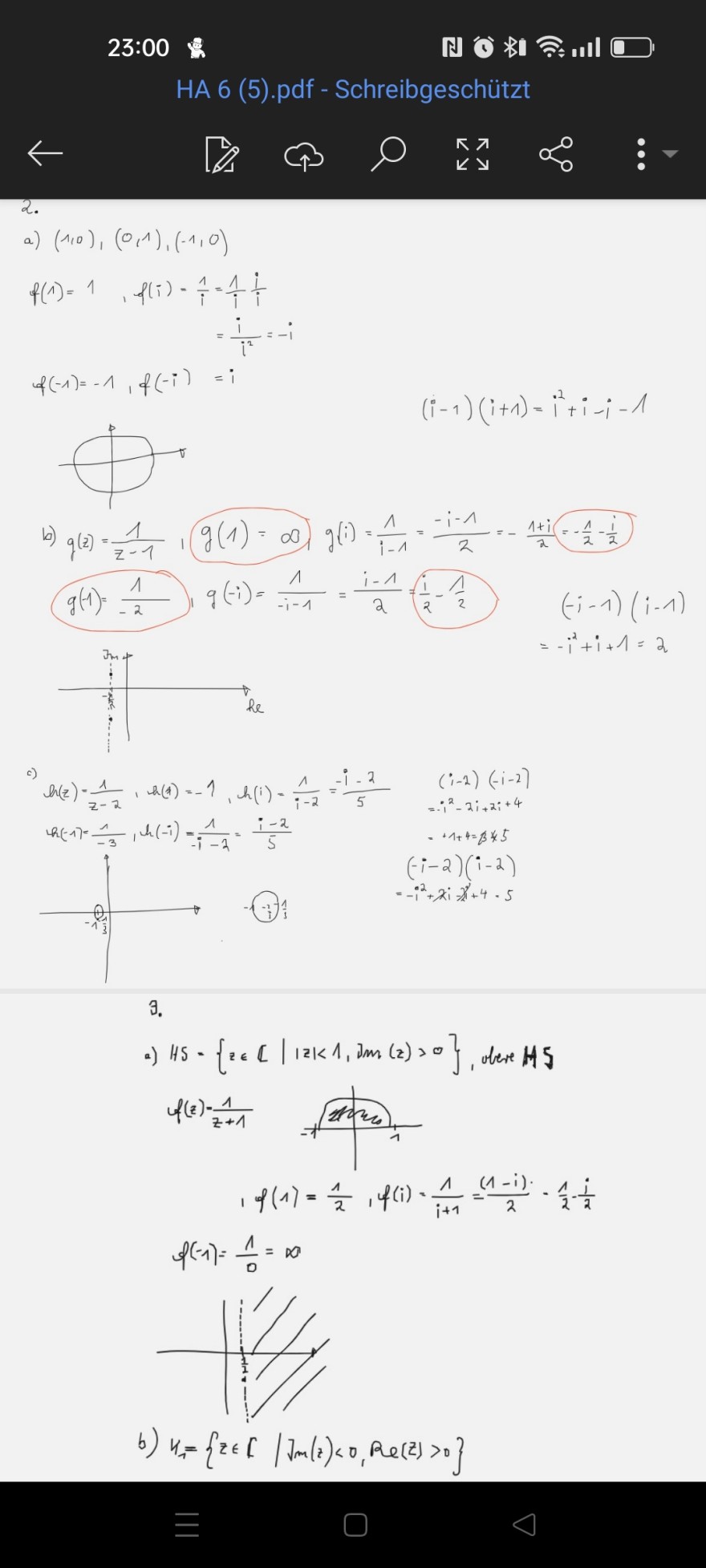
2.
\( \begin{array}{l} \text { a) }(1,0),(0,1),(-1,0) \\ f(1)=1 \quad, f(i)-\frac{1}{i}=\frac{1}{i} \frac{i}{i} \\ =\frac{i}{i^{2}}=-i \\ f(-1)=-1, f(-i)=i \\ \end{array} \)
\( (i-1)(i+1)=i^{2}+i-i-1 \)
b) \( g(z)=\frac{1}{z-1}, g(1)=\infty \quad g(i)=\frac{1}{i-1}=\frac{-i-1}{2}=-\frac{1+i}{2}=-\frac{1}{2}-\frac{i}{2} \)
\( \begin{aligned} & (-i-1)(i-1) \\ = & -i^{2}+i+1=2 \end{aligned} \)
c)
\( \text { c) } \begin{array}{l} h(z)=\frac{1}{z-2}, h(1)=-1, h(i)=\frac{1}{i-2}=\frac{-i-2}{5} \\ h(-1)=\frac{1}{-3}, h(-i)=\frac{1}{-i-2}=\frac{i-2}{5} \end{array} \)
\( \begin{aligned} & (-i-1)(i-1) \\ = & -i^{2}+i+1=2 \end{aligned} \)
\( \begin{array}{l} (i-2)(-i-2) \\ = i^{2}-2 i+2 i+4 \\ =+1+4=3 * 5 \\ (-i-2)(i-2) \\ =-i^{2}+2 i-2 x+4-5 \end{array} \)
\( =-i^{2}+x i-2 x+4-5 \)
Э.
a) \( H S=\{z \in \mathbb{C}|| z \mid<1, \operatorname{Jm}(z)>0\} \), obere \( H S \)
\( f(z)=\frac{1}{z+1} \)
\( \begin{aligned} & 1 f(1)=\frac{1}{2}, f(i)=\frac{1}{i+1}=\frac{(1-i)}{2}-\frac{1}{2}-\frac{i}{2} \\ f(-1)= & \frac{1}{0}=\infty \end{aligned} \)
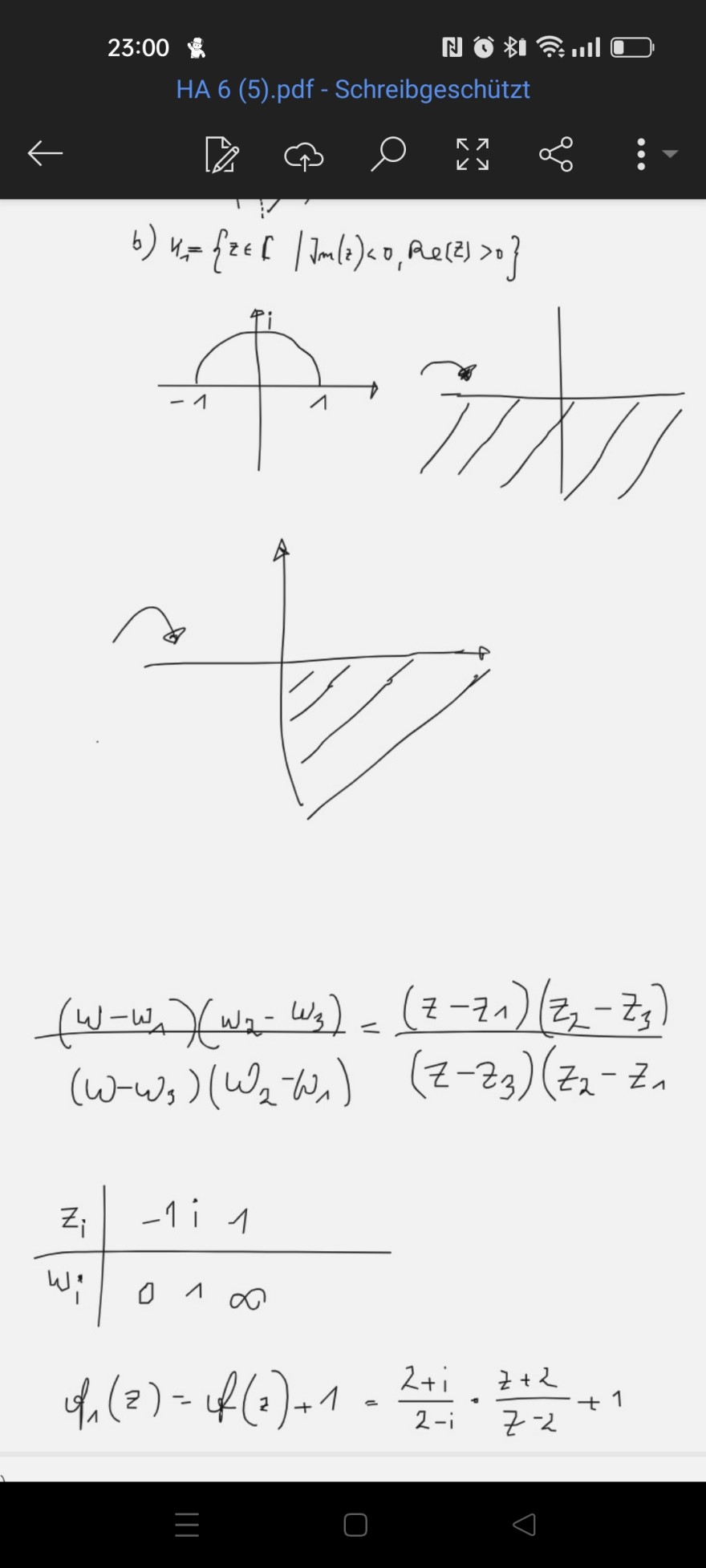
b) \( u_{1}=\left\{z \in\left[\mid J_{m}(z)<0, R e(z)>0\right\}\right. \)
Text erkannt:
23:00
HA 6 (5).pdf - Schreibgeschützt
b) \( r_{1}=\{z \in[\mid \operatorname{Jm}(z)<0, \operatorname{Re}(z)>0\} \)
\( \frac{\left(w-w_{1}\right)\left(w_{2}-w_{3}\right)}{\left(w-w_{3}\right)\left(w_{2}-w_{1}\right)}=\frac{\left(z-z_{1}\right)\left(z_{2}-z_{3}\right)}{\left(z-z_{3}\right)\left(z_{2}-z_{1}\right.} \)
\begin{tabular}{l|l}
\( z_{i} \) & \( -1 i 1 \) \\
\hline\( w_{i} \) & \( 01 \infty \)
\end{tabular}
\( f_{1}(z)=f(z)+1=\frac{2+i}{2-i} \cdot \frac{z+2}{z-2}+1 \)

Text erkannt:
\( 23: 13 \)
N な
HA 6 (5).pdf - Schreibgeschützt
\( f_{1}(z)=f(z)+1=\frac{2+i}{2-i} \cdot \frac{z+2}{z-2}+1 \)
c)
c)
\( \begin{array}{l} f_{3}(z)=\sqrt{f(z)} \quad, f(z) \\ f(z)=\left(\frac{2+i}{2-1} \cdot \frac{z+2}{z-2}\right) \\ \frac{\left(w-w_{1}\right)\left(w_{2}-w_{3}\right)}{\left(\omega-w_{3}\right)\left(w_{2}-\omega_{1}\right)}=\frac{\left(z-z_{1}\right)\left(z_{2}-z_{3}\right)}{\left(z-z_{3}\right)\left(z_{2}-z_{1}\right)} \end{array} \)
\( f(z)=\frac{(z+2)(i+2)}{(z-2)(i-2)} \)
\( \Rightarrow q(z)=\sqrt{\frac{(z+2)(i+2)}{(z-2)(i-2}} \)
d)
\( f(z)=\frac{(z+2)(i+2)}{(z-2)(i-2)} \)
Lg