Viele Schüler verwechseln das Erweitern eines Bruches mit dem Multiplizieren eines Bruches.
Beim Erweitern, bei dem Zähler und Nenner mit der gleichen Zahl multipliziert werden, ändert sich der Wert des Bruches nicht.
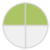
1/2 = 2/4
 =
= 
Beim Multiplizieren mit einer Zahl ungleich 1 ändert sich der Wert des Bruches.
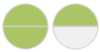
3 * 1/2 = 3/2
3 *  =
= 
2 * 9/4 = 18/4 = (18:2)/(4:2) = 9/2
2 *  =
=  =
= 