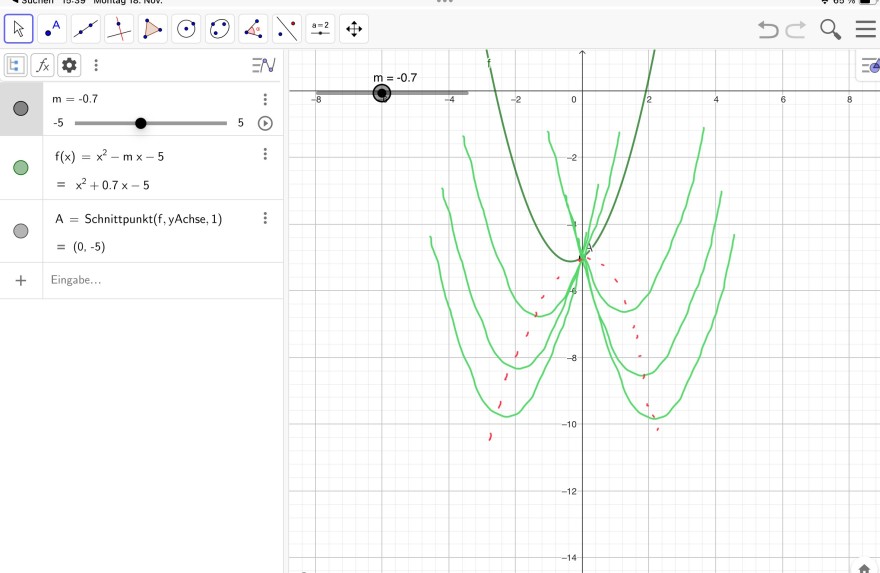
Aufgabe:
Also wir hatten die quadratische Gleichung:
x^2 -mx -5=0
Für diese sollten wir rechnerisch beweisen, dass jede quadratische Gleichung dieser Form zwei Lösungen hat.
(Kann den auch hochladen)
Und jetzt hat sie uns gezeigt auf welcher Kurve sich die möglichen Schnittpunkte dieser Parabel befinden kann (Siehe Foto)
Dafür sollen wir nun eine Funktionsgleichung angeben und es gibt scheinbar ein Verfahren mit dem es einfach ist. Ich meine dass sie etwas von „Oz-Verfahren“ genuschelt hat… Kann mir da jemand helfen?