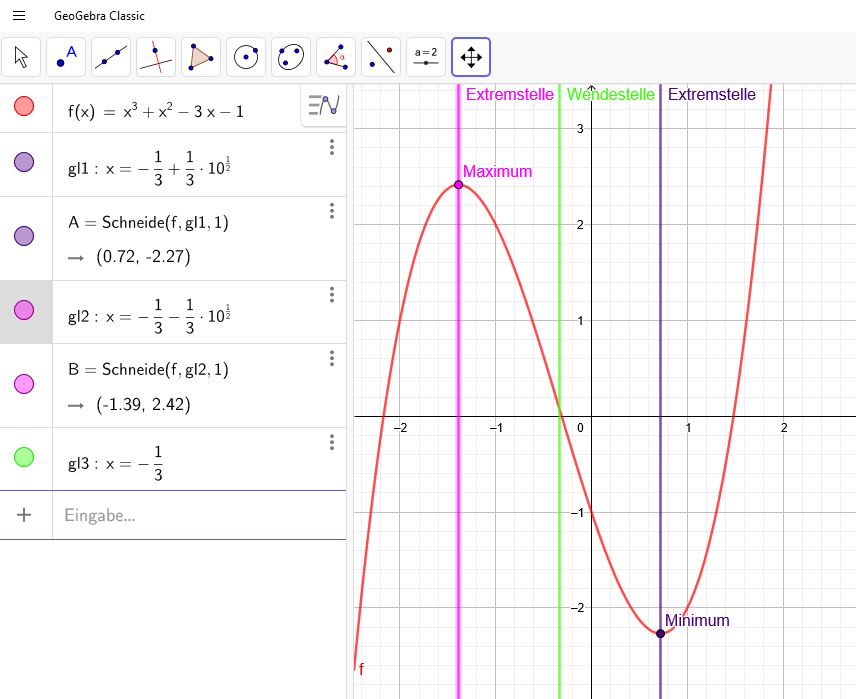
\(f(x)=x^3+x^2-3x-1\)
Extremstellenberechnung:
\(f'(x)=3x^2+2x-3\)
\(3x^2+2x-3=0|:3\)
\(x^2+\frac{2}{3}x-1=0|+1\)
\(x^2+\frac{2}{3}x=1\) quadratische Ergänzung:
\(x^2+\frac{2}{3}x+(\frac{1}{3})^2=1+(\frac{1}{3})^2\) 1.Binom:
\((x+\frac{1}{3})^2=\frac{10}{9}|±\sqrt{~~}\)
1.)
\(x+\frac{1}{3}=\frac{1}{3}\sqrt{10}\)
\(x_1=-\frac{1}{3} +\frac{1}{3}\sqrt{10}\)
2.)
\(x+\frac{1}{3}=-\frac{1}{3}\sqrt{10}\)
\(x_2=-\frac{1}{3} -\frac{1}{3}\sqrt{10}\)
Berechnung, ob lokales Maximum oder Minimum vorliegt: 2.Ableitung
\(f''(x)=6x+2\)
\(f''(-\frac{1}{3} +\frac{1}{3}\sqrt{10})\\=6\cdot (-\frac{1}{3} +\frac{1}{3}\sqrt{10})+2=2\sqrt{10}>0\) Minimum
\(f''(-\frac{1}{3} -\frac{1}{3}\sqrt{10})\\=6\cdot(-\frac{1}{3} -\frac{1}{3}\sqrt{10})+2=-2\sqrt{10}<0\) Maximum
Wendestellenberechnung:
\(f''(x)=6x+2\)→\(f''(x)=0\):
\(6x+2=0\)
\(x=-\frac{1}{3}\)