Drücke die Hypotenusenlänge eines rechtwinkligen Dreiecks durch den Inkreisradius sowie die Kathetenlängen aus. Drücke darin den Inkreisradius mit Hilfe des Umfangs aus. Forme in die am stärksten vereinfachte Form um.
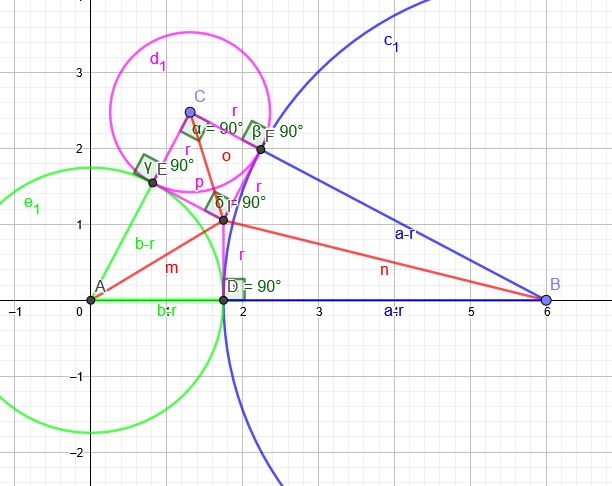
\((b-r)+(a-r)=c\)
\(b+a-2r=c\)
\(b+a-c=2r\)
\(r=\red{\frac{b+a-c}{2}}\)
Umfang:
\((b-r)+(a-r)+(a-r)+r+r+b-r=2a+2b-2r\)
\(2a+2b-2 \cdot (\red{\frac{b+a-c}{2}})=2a+2b-b-a+c=a+b+c\)