Einen Witz kann man verstehen oder auch nicht. Das Gleiche gilt für eine mathematische Aussage. Hans Aebli (Ⴕ1990) wollte daher das Erzählen von Witzen in den Mathematikunterricht aufnehmen, um bei den Schülerinnen und Schülern ein Gespür für die Inhalte des Begriffes ‚Verstehen‘ zu wecken.
Tatsächlich bedarf sowohl das Verstehen eines Witzes als auch das Verstehen einer mathematischen Aussage ein angemessenes Vorwissen. Während man aber im Zusammenhang mit mathematischem Wissen das erforderliche Vorwissen im Vorfeld bereitstellen und durchaus Entdeckerfreude erhalten kann, ist ein Bereitstellen von Vorwissen zu einem Witz ein echter Pointenkiller. Zwecks Demonstration dieses deutlichen Unterschiedes sei ein Witz erzählt, den Hans Aebli in seinem Plädoyer für das Witzeerzählen im Mathematikunterricht wiedergibt:
Zwei Kapuziner angeln am sogenannten Seedamm über den oberen Zürichsee, an dem auch ein evangelischer Pastor angelt. Als den Kapuzinern die Köder ausgehen, sagt der eine zum anderen: „Geh doch mal rüber zu der kleinen Insel. Dort findest du viele Würmer.“ Gesagt – getan: Der Kapuziner geht über das Wasser und holt Würmer. Als kurz darauf auch dem Pastor die Köder ausgehen, geht auch er los und versinkt im Wasser. Als der Pastor durchnässt den See verlassen hat, sagt der eine Kapuziner zum anderen: „Den rechten Glauben hat er wohl – aber er weiß nicht, wo die versunkenen Pfähle stehen.“
Um diesen Witz überhaupt witzig finden zu können, ist mindestens das Vorwissen erforderlich, dass Jesus auf dem Wasser wandelte. Zusätzlich kann es nicht schaden zu wissen, dass sich Katholiken und Protestanten gegenseitig hinsichtlich der Glaubenstiefe misstrauen – insbesondere dann, wenn es um den Glauben an Wunder geht. Und ganz besonders lebt dieser Witz von einem Insiderwissen über den Ort, an dem sich der Witz ereignet. Am Seedamm über den oberen Zürichsee sind Reste von Stützpfeilern einer Brücke unter der Wasseroberfläche verborgen. Wollte man einem weder bibelfesten noch ortskundigen Zuhörer all dies vor der Erzählung bereitstellen wäre dem Witz jegliche Spitze abgebrochen.
Ganz anders verhält es sich beim Verstehen einer mathematischen Aussage. Auch hier ein Beispiel:
Die Summe der Flächeninhalte der Quadrate über den Katheten eines rechtwinkligen Dreiecks ist gleich dem Flächeninhalt des Quadrats über der Hypotenuse diese Dreiecks.
Ein Verstehen dieser Aussage liegt dann vor, wenn Einsicht in das ‚Warum‘ dieser Aussage erzeugt wurde. Da vermutlich kaum ein Schüler oder eine Schülerin selbständig zu dieser Einsicht gelangen wird, können Lehrer*innen zum Beispiel diese Skizze vorgeben:
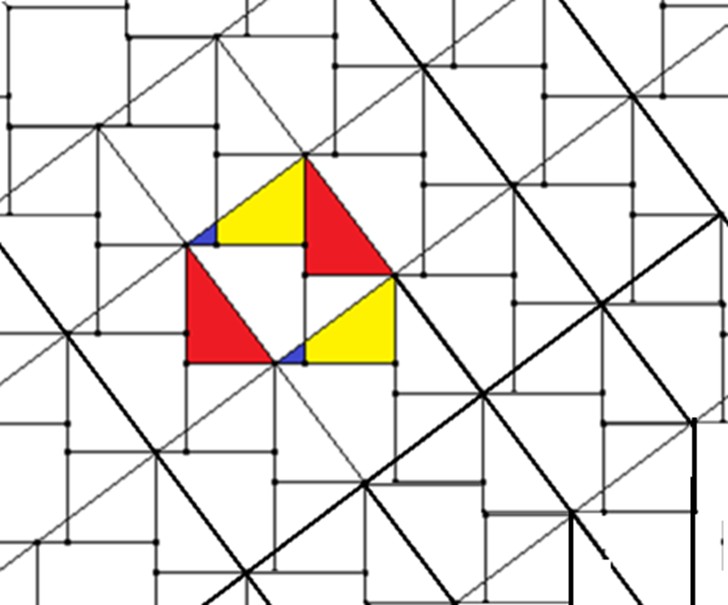
Die Einsicht in das ‚Warum‘ kann auf diese Weise selbständig erworben werden, ohne den Schüler*innen den Spaß an der Sache zu verderben.
Es kann an dieser Stelle allerdings Schüler*innen geben, welche wissen möchten, wie man auf eine derartige Skizze kommt. Dieser Gedanke weist auf eine weitere Dimension des Verstehens hin, die im Zusammenhang mit dem Verstehens eines Witzes ohne Belang ist. Aeblis hübsche Idee, den Vorgang des Verstehens über das Witzeerzählen zugänglich zu machen, hat nur die Verstehensdimension des ‚Warum?‘ im Blick. Die zweite, ebenso wichtige Verstehensdimension, die gute Idee, der geniale Gedanke oder der Geistesblitz wird nicht nur bei Aebli sondern allgemein in der Didaktik kaum in den Blick genommen.
Das kann daran liegen, dass es eine Didaktik des genialen Gedanken nicht geben kann, weil Geistesblitze nicht in der Weise vermittelbar sind, wie die meisten schulmathematischen Inhalte. Geistesblitze erfordern einen umfangreichen Erfahrungshintergrund, Hartnäckigkeit im Verfolgen einer Problemlösung und letztlich auch ein Wechsel zwischen Phasen der Anspannung und der Entspannung. Der Geistesblitz stellt sich sprichwörtlich oft erst ‚über Nacht‘ ein – und das auch nur, wenn man sich tagsüber intensiv mit einem Problem beschäftigt hat und umfangreiche Erfahrungen in Ruhephasen Gelegenheit erhalten, mit Lösungsgedanken Synapsen zu bilden.