Verteilungstest. Chi-Quadrat Test Aufgabe 51

Question

Aufgabe:

Es geht um die Verteilungstests (CHI-Quadrat). Soweit bin ich gekommen. Stimmt meine bisherige Vorgehensweise? Und wie soll ich weiterrechnen ohne dass alpha gegeben ist?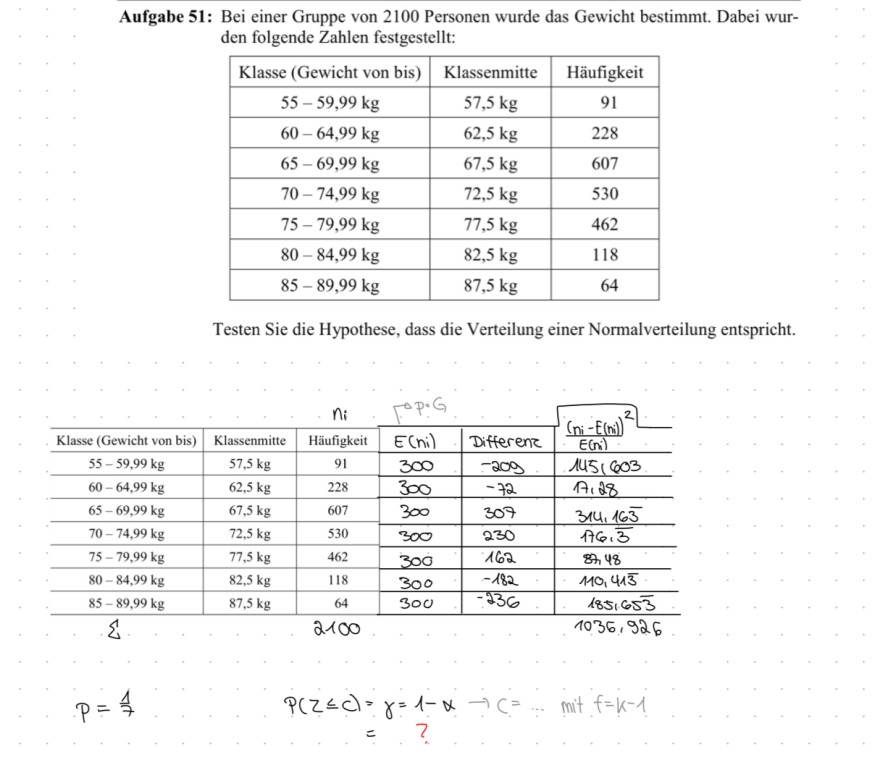

Text erkannt:

Aufgabe 51: Bei einer Gruppe von 2100 Personen wurde das Gewicht bestimmt. Dabei wurden folgende Zahlen festgestellt:
\begin{tabular}{|c|c|c|}
\hline Klasse (Gewicht von bis) & Klassenmitte & Häufigkeit \\
\hline $55-59,99 \mathrm{~kg}$ & $57,5 \mathrm{~kg}$ & 91 \\
\hline $60-64,99 \mathrm{~kg}$ & $62,5 \mathrm{~kg}$ & 228 \\
\hline $65-69,99 \mathrm{~kg}$ & $67,5 \mathrm{~kg}$ & 607 \\
\hline $70-74,99 \mathrm{~kg}$ & $72,5 \mathrm{~kg}$ & 530 \\
\hline $75-79,99 \mathrm{~kg}$ & $77,5 \mathrm{~kg}$ & 462 \\
\hline $80-84,99 \mathrm{~kg}$ & $82,5 \mathrm{~kg}$ & 118 \\
\hline $85-89,99 \mathrm{~kg}$ & $87,5 \mathrm{~kg}$ & 64 \\
\hline
\end{tabular}

Testen Sie die Hypothese, dass die Verteilung einer Normalverteilung entspricht.
$p=\frac{1}{7}$
$\begin{aligned} P(z \leqslant c) & =\gamma=1-\alpha \rightarrow c=\ldots \text { mit } f=k-1 \\ & =? \end{aligned}$

Comments

Du gehst bei der Berechnung der erwarteten Häufigkeiten von einer Gleichverteilung aus. Das ist verkehrt. Du musst natürlich die Parameter der Normalverteilung aus der Stichprobe ermitteln und damit die erwarteten Häufigkeiten ermitteln.

---

Und wie genau geht das ? Ich bräuchte es glaube ich an der Aufgabe erklärt um es richtig zu verstehen.

---

Fang damit an, die Parameter der Normalverteilung aus der Stichprobe zu ermitteln.