italienische Firma untersucht das Füllgewicht von Kaffeepackungen

Question

Aufgabe:

Eine italienische Firma untersucht das Füllgewicht von Kaffeepackungen einer bestimmten Marke. Das auf der Verpackung angegebene Gewicht beträgt 1000g. Es wird angenommen das Füllgewicht sei normalverteilt. Eine Stichprobe aus 24
Kaffeepackungen ergibt ein durchschnittliches Füllgewicht von 1070g und eine empirische Varianz von 20671g
.Geben Sie die Obergrenze des 90%-Konfidenzintervalls für das durchschnittliche Füllgewicht der Kaffeepackungen an.

Problem/Ansatz:

Ich bereite mich gerade auf die Prüfung vor und versuche schon seit einer Weile, diese Aufgabe zu lösen, aber ich komme einfach nicht auf das richtige Ergebnis. Könnte mir jemand den Lösungsweg Schritt für Schritt erklären?

danke

Answer 1

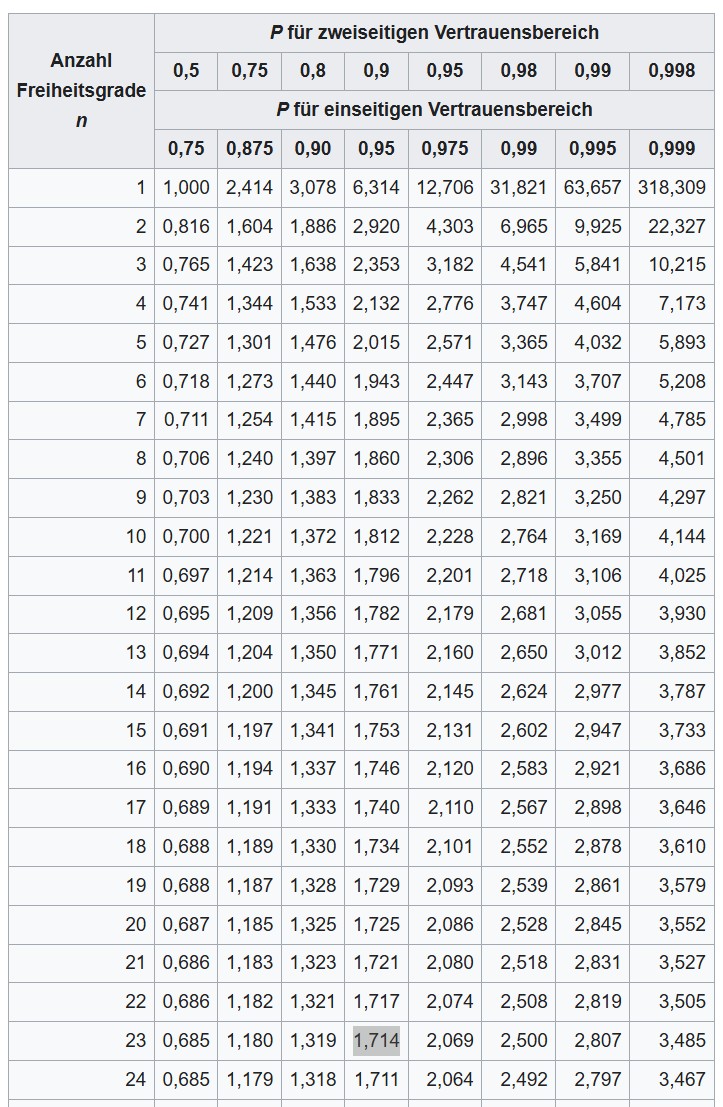
Rechnung über die t-Verteilung, wenn die Standardabweichung der Grundgesamtheit aus der Stichprobe geschätzt wird.

Untergrenze: 1070 - 1,71387152774705 * √20671 / √24 = 1019,70169076351

Obergrenze: 1070 + 1,71387152774705 * √20671 / √24 = 1120,29830923649

Länge: 2 * 1,71387152774705 * √20671 / √24 = 100,596618472972

Wenn ihr keinen Rechner benutzen dürft, der die t-Verteilung integriert hat, kann man den Wert in einer Tabelle nachschlagen.