Löse die folgende Exponentialgleichungen

Question

Wie kann ich folgende Exponentialgleichungen nach x auflösen:

a) \( e^{x}=4 \)
e) \( 1,5 \mathrm{e}^{-0,5 x}-1=1 \)
b) \( e^{2 x}=2 \)
f) \( e^{5 x}+5=5 e^{5 x} \)
c) \( 66 e^{4 x}=132 \)
g) \( 1,04^{x}=1,3685695 \)
d) \( 5-e^{0,25 x}=0,1 \)
h) \( 0,123 \cdot 3^{x}=269,001 \)

Answer 1

Jede Gleichung die das x nur an einer Stelle enthält, kann über Äquivalenzumformungen direkt zum x aufgelöst werden.

e^x = 4
x = ln(4)

1.5*e^{-0.5x} - 1 = 1
1.5*e^{-0.5x} = 2
e^{-0.5x} = 2/1.5 = 4/3
-0.5x = ln(4/3)
x = -2ln(4/3)

e^{2x} = 2
2x = ln(2)
x = ln(2)/2

Versuche diese ersten 3 Gleichungen mal nachzuvollziehen und dann alle anderen bis auf f) zu machen. Das solltest du vermutlich schaffen. Wenn nich frag gerne nach. Bei f) muss man zunächst vereinfachen

e^{5x} + 5 = 5e^{5x}
5 = 4e^{5x}

Dann sollte auch f) weniger Probleme machen.

Comments

vielen dank, das werde ich machen

---

Es gibt sonst ja auch Hilfsprogramme wie Photomath, Wolframalpha etc., die genau bei solchen Aufgaben helfen können. Ich weiß nicht, ob KI schon zuverlässig solche Aufgaben rechnen kann. Kann man aber auch mal probieren.

Hier mal ein Versuch mit ChatGPT. Und ChatGPT ist inzwischen rechnerisch schlechter als DeepSeek.

Wir lösen die Gleichung:

$$ 1.5 \cdot e^{-0.5x} - 1 = 1 $$

### Schritt 1: Umformen der Gleichung
$$ 1.5 \cdot e^{-0.5x} - 1 = 1 $$
Addiere 1 auf beiden Seiten:
$$ 1.5 \cdot e^{-0.5x} = 2 $$

### Schritt 2: Beide Seiten durch 1.5 teilen
$$ e^{-0.5x} = \frac{2}{1.5} = \frac{4}{3} $$

### Schritt 3: Logarithmieren (natürlicher Logarithmus \(\ln\))
$$ -0.5x = \ln\left(\frac{4}{3}\right) $$

### Schritt 4: Nach \(x\) auflösen
$$ x = \frac{-2 \cdot \ln\left(\frac{4}{3}\right)}{1} $$

Das ist die exakte Lösung. Wenn wir die Lösung numerisch berechnen:
$$ x \approx -0.81093 $$

Du sieht größtenteils sieht das schon recht gut aus. Nur ist ChatGPT leider nicht in der Lage den Logarithmus richtig numerisch wie der Taschenrechner auszurechnen. Das macht DeepSeek z.B. besser.

---

@MC würde die f so stimmen?

\( e^{5 x}+5=5 e^{5 x} \)   /   -e^5x

5 = 4e^5x  / :4

5/4 = e^5x   /ln

ln(5/4) = 5 * x / :5

x = ln(5/4) / 5

---

Ja, geht doch…

Answer 2

c)

\( 66 e^{4 x}=132|:66 \)

\(  e^{4 x}=2 \)

Weitere Möglichkeit über Substitution mit \(4x=u\):

\(  e^{u}=2 \)

\(  u\cdot \ln(e)=\ln(2) \)   mit \(  \ln(e)=1\):

\(  u=\ln(2) \)  Re-Substitution:

\(  4x=\ln(2)|:4 \)

\(  x=\frac{\ln(2)}{4}\)

h)

 \( 0,123 \cdot 3^{x}=269,001|: 0,123\)

\(  3^{x}=269,001|: 0,123\)

\(  3^{x}=2187\)

\(  x\cdot\ln(3)=\ln(2187)\)

\(  x=\frac{\ln(2187)}{\ln(3)}\)

Es ist auch  \(2187=81\cdot 27=3^4\cdot 3^3=3^7\)

\(x=7\)

d)

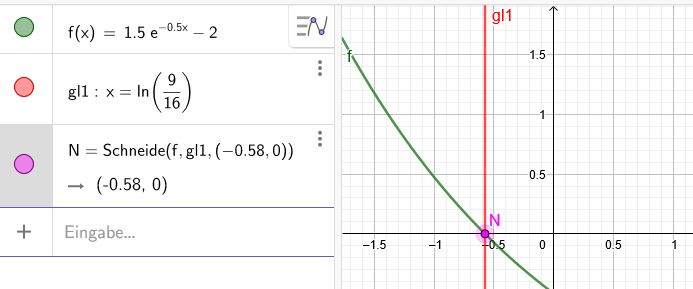
\( 1,5 \mathrm{e}^{-0,5 x}-1=1  |+1 \)

\( 1,5 \mathrm{e}^{-0,5 x}=2|:1,5 \)

\( {e}^{-0,5 x}=\frac{2}{1,5}=\frac{20}{15}=\frac{4}{3} \)

\( \frac{1}{{e}^{0,5 x}}=\frac{4}{3} \) Über Kreuzmultiplikation:

\( 4\cdot {e}^{0,5 x} =3|:4 \)

\( {e}^{0,5 x} =\frac{3}{4} \)

\( 0,5 x =\ln(\frac{3}{4}) \)

\(  x =\red{2}\cdot \ln(\frac{3}{4})=\ln((\frac{3}{4})^\red{2})=\ln(\frac{9}{16}) \)