Aufgabe:
Problem/Ansatz:
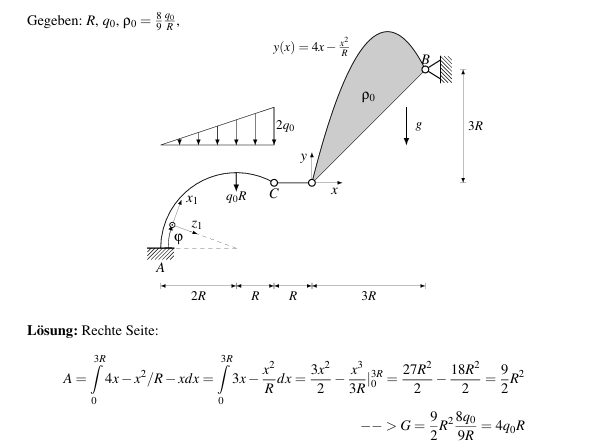
Hallo, ich hätte hier eine Frage zu der berechneten grau gefärbten Fläche.
Mein Ansatz war hier ähnlich wie in der Lösung:
Grenzen von 0 bis 3R und die Funktion y(x) einsetzten, integrieren und dann eine zweite Berechnung machen. Diese soll das Dreieck unterbei sein, heißt 3R + 3R und dann diese 9R²/2 von der ersten Fläche abziehen.
Jetzt wurde bei dem Integral noch ein -x hinzugefügt.
Steht das für die untere Fläche die ich extra berechnet habe?
Ich komme jedenfalls nicht aufs gleiche.
Wenn ich die funktion integriere und dann von 0 bis 3R dann berechne ich ja die gesamte heißt ich muss das Eck ja noch abziehen??
Übersehe ich hier etwas? Danke schonmal :)
Text erkannt:
Gegeben: \( R, q_{0}, \rho_{0}=\frac{8}{9} \frac{q_{0}}{R} \),
Lösung: Rechte Seite:
\( \begin{array}{l} A=\int \limits_{0}^{3 R} 4 x-x^{2} / R-x d x=\int \limits_{0}^{3 R} 3 x-\frac{x^{2}}{R} d x=\frac{3 x^{2}}{2}-\left.\frac{x^{3}}{3 R}\right|_{0} ^{3 R}=\frac{27 R^{2}}{2}-\frac{18 R^{2}}{2}=\frac{9}{2} R^{2} \\ -->G=\frac{9}{2} R^{2} \frac{8 q_{0}}{9 R}=4 q_{0} R \end{array} \)