Text erkannt:
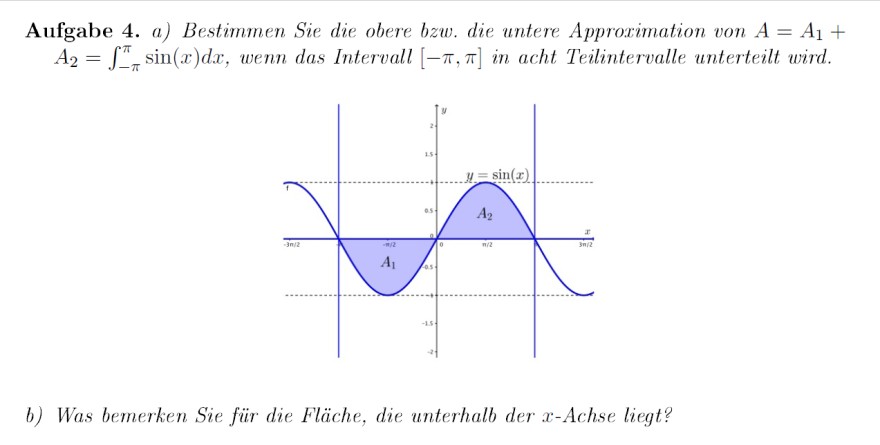
Aufgabe 4. a) Bestimmen Sie die obere bzw. die untere Approximation von \( A=A_{1}+ \) \( A_{2}=\int \limits_{-\pi}^{\pi} \sin (x) d x \), wenn das Intervall \( [-\pi, \pi] \) in acht Teilintervalle unterteilt wird
b) Was bemerken Sie für die Fläche, die unterhalb der \( x \)-Achse liegt?
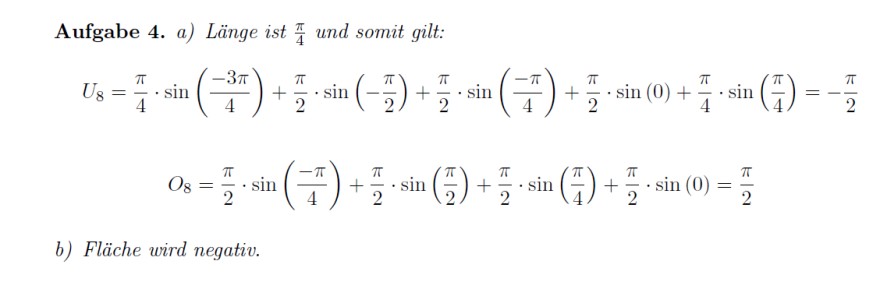
Text erkannt:
Aufgabe 4. a) Länge ist \( \frac{\pi}{4} \) und somit gilt:
\( \begin{array}{c} U_{8}=\frac{\pi}{4} \cdot \sin \left(\frac{-3 \pi}{4}\right)+\frac{\pi}{2} \cdot \sin \left(-\frac{\pi}{2}\right)+\frac{\pi}{2} \cdot \sin \left(\frac{-\pi}{4}\right)+\frac{\pi}{2} \cdot \sin (0)+\frac{\pi}{4} \cdot \sin \left(\frac{\pi}{4}\right)=-\frac{\pi}{2} \\ O_{8}=\frac{\pi}{2} \cdot \sin \left(\frac{-\pi}{4}\right)+\frac{\pi}{2} \cdot \sin \left(\frac{\pi}{2}\right)+\frac{\pi}{2} \cdot \sin \left(\frac{\pi}{4}\right)+\frac{\pi}{2} \cdot \sin (0)=\frac{\pi}{2} \end{array} \)
b) Fläche wird negativ.
Problem/Ansatz: Kann mir jemand erklären wie er auf die verschiedenen Pi-Werte kommt, wenn das Intervall (Pi, -Pi) durch achtgeteilt wird? Warum ist es nicht immer Pi-Achtel sein?