Hallo zusammen!
Ich bin gerade in Algebra bei der Galoistheorie angelangt und ich habe jetzt gerade die Galoiskorrespondenz "kennengelernt":
Satz 3.5.1 (Galoiskorrespondenz). Sei \( L / K \) eine Galoiserweiterung mit Galoisgruppe \( G=G(L / K) \). Dann sind die Abbildungen
\( \varphi: \mathcal{U}(G) \rightarrow \mathcal{Z}(L / K), H \mapsto L^{H} \)
und
\( \psi: z(L / K) \rightarrow \mathcal{U}(G), M \mapsto G(L / M) \)
zueinander inverse Bijektionen.
Nun haben wir auch noch ein Bsp. gehabt, welches ich allerdings nicht ganz verstehe:
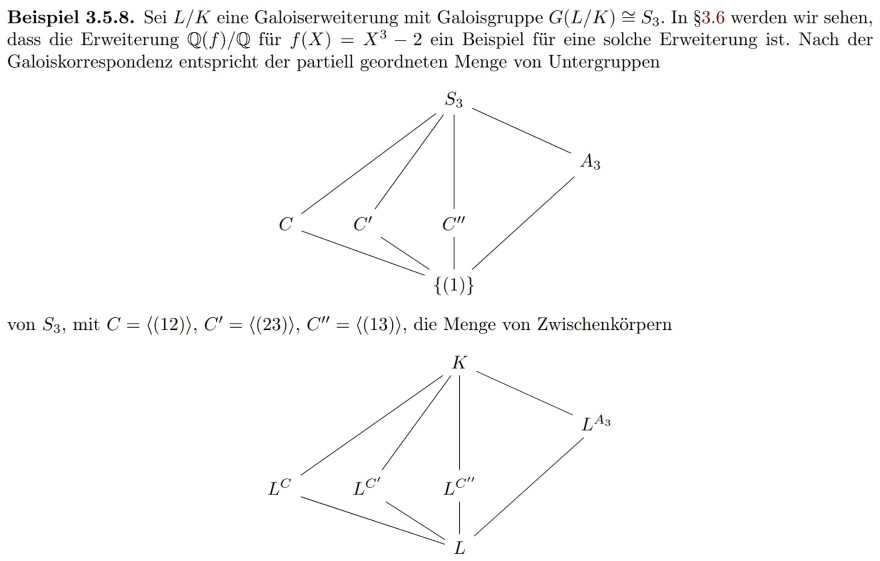
von \( L / K \). Dabei ist die Erweiterung \( L^{A_{3}} / K \) galoissch mit Galoisgruppe \( S_{3} / A_{3} \cong C_{2} \). Die restlichen Zwischenkörper \( L^{C}, L^{C^{\prime}} \) und \( L^{C^{\prime \prime}} \) sind nicht galoissch: Die zugehörigen Gruppen \( C, C^{\prime} \) und \( C^{\prime \prime} \) sind kongugiert so dass die Zwischenkörper \( L^{C}, L^{C^{\prime}} \) und \( L^{C^{\prime \prime}} \) also isomorph über \( K \) sind. Vom Standpunkt der \( G \)-Wirkungen aus Bemerkung 3.5.6 wirkt die Gruppe \( S_{3} \) mit Fixpunkt \( A_{3} \) (bzw. \( L^{A_{3}} \) ) und durch zyklische Permutation der Untergruppen Gruppen \( C, C^{\prime} \) und \( C^{\prime \prime} \) (bzw. \( L^{C}, L^{C^{\prime}} \) und \( L^{C^{\prime \prime}} \) ).
Dabei verstehe ich nicht, warum nur die Erweiterung \(L^{A_3}/K\) galoissch sein soll, aber eben die anderen nicht und wie man überhaupt das zeigen kann, dass jene Erweiterung galoissch ist?
Ich wäre über jede Idee dankbar!
Vielen Dank im Voraus!