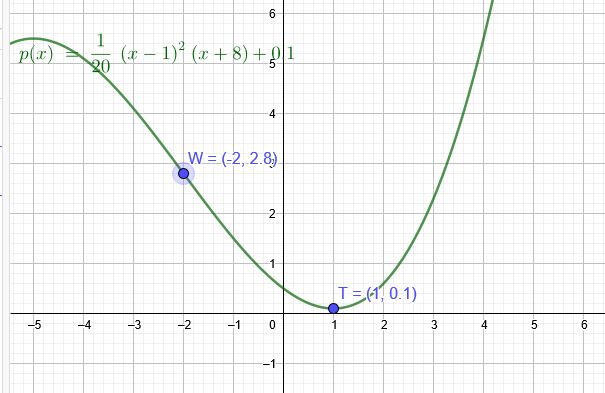
Die Funktion f ist eine ganzrationale Funktion dritten Grades. Der Graph hat den Wendepunkt \(W(-2|2,8)\) und den Tiefpunkt \(T (1|0,1)\)
Ich verschiebe den Graphen um 0,1 Einheiten nach unten:
\(W(-2|2,8)\)→\(W´(-2|2,7)\) \(T (1|0,1)\)→ \(T ´(1|0)\)
\(f(x)=a*(x-1)^2*(x-N)\)
\(W´(-2|2,7)\):
\(f(-2)=a*(-2-1)^2*(-2-N)=2,7\)
\(9a*(-2-N)=2,7\) →\(a=-\frac{0,3}{(2+N)}\)
\(f(x)=-\frac{0,3}{(2+N)}*[(x-1)^2*(x-N)]\)
\(f´(x)=-\frac{0,3}{(2+N)}*[(2x-2)*(x-N)+(x-1)^2]\)
\(f´´(x)=-\frac{0,3}{(2+N)}*[2*(x-N)+(2x-2)+(2x-2)]\)
\(W´(-2|....)\):
\(f´´(-2)=-\frac{0,3}{(2+N)}*[2*(-2-N)+(2*(-2)-2)+(2*(-2)-2)]\)
\(-\frac{0,3}{(2+N)}*[2*(-2-N)+(2*(-2)-2)+(2*(-2)-2)]=0\)
\(N=-8\) \(a=-\frac{0,3}{(2-8)}=\frac{0,3}{6}=\frac{1}{20}\)
\(f(x)=\frac{1}{20}*(x-1)^2*(x+8)\)
Wieder 0,1 Einheiten nach oben:
\(p(x)=\frac{1}{20}*(x-1)^2*(x+8)+0,1\)