Hi,
vllt nochmals in einfacheren Worten (Du wirst nicht wissen was "injektiv" bedeutet oder was mit w. H. gemeint ist ;)).
Eine Umkehrfunktion ist graphisch gesehen eine Spiegelung an der ersten Winkelhalbierenden (bei immai mit 1. w. H. abgekürzt).
Siehe dazu auch hier rein: http://www.brinkmann-du.de/mathe/gost/p0_umkehrfunktionen_01.htm
Sind ein paar Beispiele dabei ;).
Das bedeutet eigentlich nichts anderes, als das x- und y-Werte vertauscht werden. Das ist auch die Hauptaufgabe bei solchen Funktionen -> Nach der anderen Variablen auflösen (siehe ebenfalls Link).
Was immai weiterhin meinte, ist das man aufpassen muss von was man die Umkehrung bildet, da es zu Problemen kommen kann. Spiegelt man mal die Funktion f(x) an der 1. Winkelhalbierenden sieht das so aus:
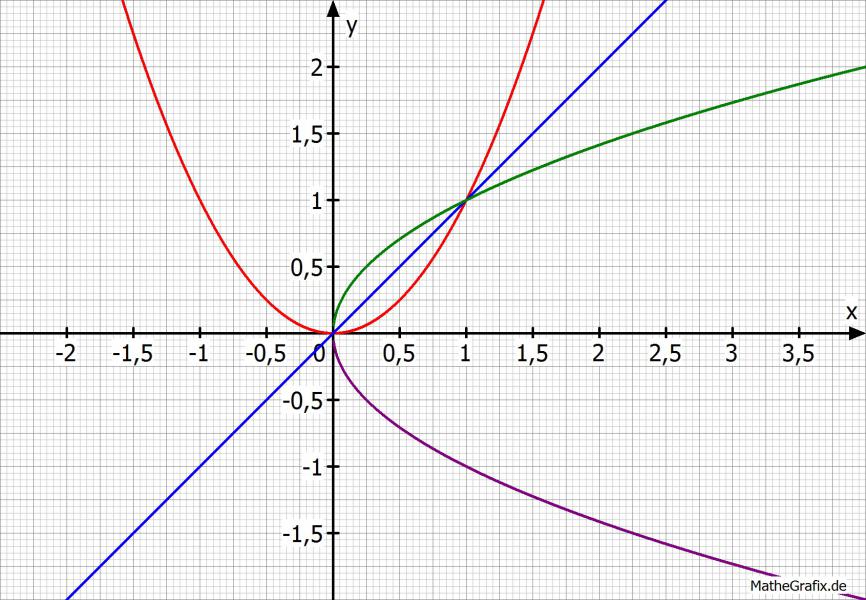
Wie Du siehst entspricht der grüne und violette Graph dem "umgefallenen" Graphen von x^2. Doch ist das keine Funktion mehr, da zwei y-Werte an der gleichen Stelle x angenommen werden. Hier muss also zuvor die Bedingung geschaffen werden, dass man sagt man betrachtet nur x≥0 und hat am Ende nur den grünen Graphen! (Siehe auch dazu nochmals den obigen Link).
Zum Abschluss noch: Die Umkehrfunktion wird durch ein hochgesetztes (-1) deutlich gemacht. Also
Funktion: f(x)
Umkehrfunktion: f^{-1}(x)
Beachte, dass das dabei kein Exponent ist, also i.A. f^{-1}(x) ≠ 1/f(x).
Grüße