Limes von Funktion f(x):= -(x^2 + x -4)/(√(4-x^2)) berechnen

Question

stehe gerade auf dem Schlauch, oder die Aufgabe ist schwer:

Ich möchte den Limes für x gegen -2 und x gegen 2 von $$- \frac{ x^2 + x - 4 }{ \sqrt{ 4 - x^2 } }$$ berechnen.

Ich kriege es aber einfach nicht hin.

Hat jemand einen Tipp?

Danke,

Thilo

Comments

Die funktion darf doch gar nicht minus 2 plus 2 werden. Bei x=1.9 lauft es -2.5 Bei x=-1.9 gegen 3.7.

---

D = (-2,2)

Wenn du oben und unten quadrierst und dann noch Zähler und Nenner durch x^2 teilst, siehst du schon mal, dass da eine unbeschränkte Zahl rauskommt.

Das Vorzeichen musst du dann aber ohne Quadrieren finden und ist allein bestimmt durch das Vorzeichen des ursprünglichen Zählers, das ja im betrachten Definitionsbereich wechselt.

Answer 1

f(x) = - (x^2 + x - 4)/√(4 - x^2)

Betrachte mal den Grenzwert von Zähler und Nenner getrennt

lim (x→2) -(x^2 + x - 4) = -2

lim (x→-2) -(x^2 + x - 4) = 2

lim (x→2) √(4 - x^2) = 0

lim (x→-2) √(4 - x^2) = 0

Und jetzt den Grenzwert zusammen. Wenn man eine Zahl ungleich Null durch 0 teilt kommt als Betrag unendlich heraus.

lim (x→2) - (x^2 + x - 4)/√(4 - x^2) = -∞

lim (x→-2) - (x^2 + x - 4)/√(4 - x^2) = ∞

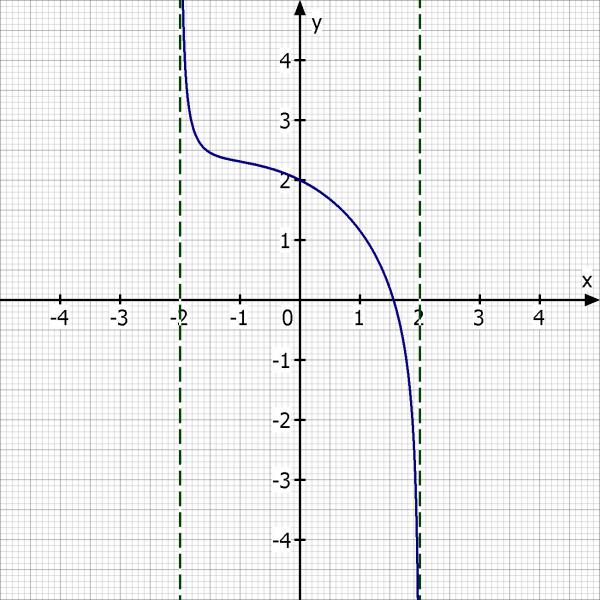
Skizze

Comments

Darf man denn das so machen?

Du schaust nicht nach rechts bzw. links von der Stelle -2 bzw. 2.

Wenn Du genauso bei f(x) = (x+1)/(x-1) vorgehen würdest, würde das zu keinem guten Ende kommen.


Grüße

---

Grundsätzlich kann die Wurzel selber nur Positiv sein. Dazu muss der Radikand nicht negativ sein. Ich war mal davon ausgegangen das man sieht das der Definitionsbereich -2 ≤ x ≤ 2 ist.

---

Danke :)     .

---

Hmm, ja, ich hatte mir die Funktion ja auch gezeichnet und gesehen, dass sie höchstwahrscheinlich gegen += unendlich geht für x gegen -+2. Aber bin mir auch nicht sicher, ob man das so machen darf. Wie Unknown schon meinte, bei manch anderen Funktionen funktioniert das so nicht.

---

Wie gesagt eine Wurzel kann nicht negativ werden Daher kann sich das Vorzeichen nicht umdrehen.

Das wäre wenn dann zu einem Fall ähnlich wie 

(x+1) / |x-1|

Also wenn du unter dem Bruch einen Betrag hast. Da brauch ich grundsätzlich nichts unterscheiden. Ich sehe bei 1 wird der Nenner 0. D.h. in der unmittelbaren umgebung 0+.

Da im Zähler eine 2 steht ist das also +∞ als grenzwert. Und zwar egal ob wir uns von links oder rechts nähern. Daher brauche ich das bei der Wurzel auch nicht näher untersuchen. 

---

Echt interessant. Aber als ich es im gtrr eingab kammen diese grenzen, also hat mein gtr falsch eingezeigt?

---

Setze mal +-1.999 ein.

---

Also statt 1.9 1.99 und dann vergleichen?