Das ist wirklich seltsam.
Ist das deine Annahme, weil keine Grenzen angegeben sind ? 0<x<1
Die Kurve sieht ja so aus:
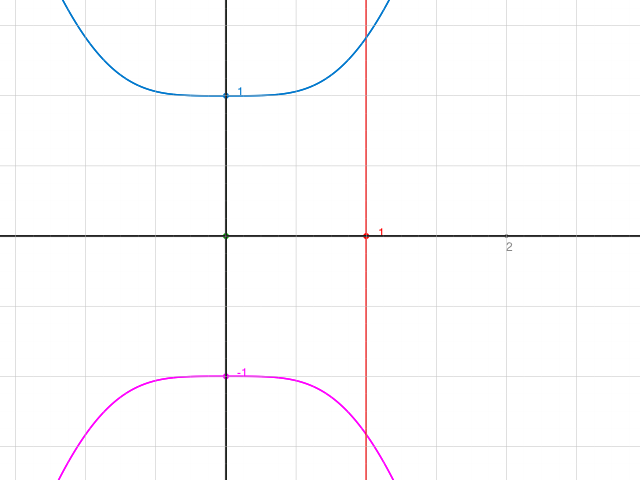
Hast du da nirgends ein Minus übersehen? Oder hast du einen Hinweis auf Symmetrie? Wenn nicht, musst du wohl einfach mal Grenzen a und b nehmen. Dann hast du halt ein Resultat mit a und b.
Eine Formel zur Berechnung des Schwerpunkts von Rotationskörpern hast du hoffentlich.
Falls da 0<x<1 angegeben ist, kannst du a=0 und b=1 wählen.
