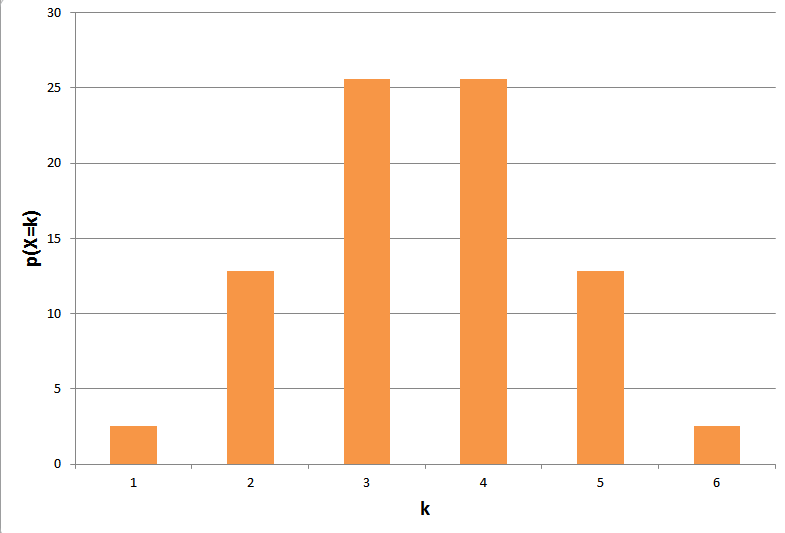Wahrscheinlichkeit: Tierarzt untersucht Rinderkrankheit

Question

Wahrscheinlichkeitsaufgabe über einer Rinderkrankheit:

Ein Tierarzt untersucht \( n=5 \) Rinder, die mit einer Wahrscheinlichkeit von \( p=0,2 \) unter einer bestimmten Krankheit leiden.

(a) Berechnen Sie die Wahrscheinlichkeiten, dass \( \underline{k}=0,1,2,3,4,5 \), Tiere erkrankt sind!

(b) Stellen Sie diese Verteilung grafisch dar (x-Achse: \( k \), y-Achse: \( p(X=k)) ! \)

(c) Wie würde sich das Bild verändern, wenn die Krankheitswahrscheinlichkeit \( p=0,5 \) bzw. \( p=0,7 \) wäre (keine explizite Rechnung erforderlich)?

Meine Lösungen:

a)
\( P(X=k)=\left(\begin{array}{l}n \\ k\end{array}\right) * p^{2 *} q^{2} \)
\( P(X=0)=\left(\begin{array}{l}5 \\ 0\end{array}\right) * p^{2 *} q^{2}=1 *(0,2)^{2} *(0,8)^{2}=0,0256 \approx 2,56 \% \)
\( P(X=1)=\left(\begin{array}{c}5 \\ 1\end{array}\right) * p^{2 *} q^{2}=5 *(0,2)^{2 *}(0,8)^{2}=0,128 \approx 12,8 \% \)
\( P(X=2)=\left(\begin{array}{l}5 \\ 2\end{array}\right) * p^{2 *} q^{2}=10 *(0,2)^{2 *}(0,8)^{2}=0,256 \approx 25,6 \% \)
\( P(X=3)=\left(\begin{array}{l}5 \\ 3\end{array}\right) * p^{2 *} q^{2}=10 *(0,2)^{2} *(0,8)^{2}=0,256 \approx 25,6 \% \)
\( P(X=4)=\left(\begin{array}{l}5 \\ 4\end{array}\right) * p^{2 *} q^{2}=5 *(0,2)^{2 *}(0,8)^{2}=\approx 0,128 \approx 12,8 \% \)
\( P(X=5)=\left(\begin{array}{l}5 \\ 5\end{array}\right) * p^{2 *} q^{2}=1 *(0,2)^{2} *(0,8)^{2}=0,0256 \approx 2,56 \% \)
c) \( p=0,5 \)
0,0625
\( \Rightarrow 2 \) mal \( 6,25 \% ; 2 \) mal \( 31,25 \% ; 2 \) mal \( 62,5 \% \)
\( p=0,7 \)
0,0441
\( \Rightarrow 2 \) mal \( 4,41 \% ; 2 \) mal \( 22,05 \% ; 2 \) mal \( 44,1 \% \)

b)

Answer 1

Man rechnet mit der Binomialverteilung

Achtung die Exponenten von p und q ändern sich auch immer !!

P(X = k) = COMB(5, k) · 0.2^k · 0.8^{5 - k}

[0, 0.32768;
1, 0.4096;
2, 0.2048;
3, 0.0512;
4, 0.0064;
5, 0.00032]

Wenn p = 0.5 ist, wird die Verteilung flacher und der Erwartungswert verschiebt sich in die Mitte

Wenn p = 0.7 ist wird die Verteilung wieder spitzer und der Erwartungswert verschiebt sich noch weiter nach rechts.

Comments

auch hier vielen Dank für deine turboschnelle Antwort! Okay, in Zukunft weiß ich Bescheid, dass man q^n-k rechnen muss! Ich habe unten den korrigierten Graphen im Anhang.

---

Oh. Achte mal auf die Beschriftung. Die Balken sind mit 1 bis 6 beschriftet. Richtig wäre allerdings 0 bis 5.

Der Erwartungswert E(x) = n * p = 5 * 1/5 = 1 sollte im Balkendiagramm den höchsten Wert haben.

Darüber bin ich gerade gestolpert und habe gesehen das da irgendwas nicht stimmen kann.

---

Korrektur des Graphen:

 

Answer 2

 

Du hast die Binomialverteilung leider nicht richtig berechnet; man kann sich das so verdeutlichen: Wenn wir eine geringe Wahrscheinlichkeit der Erkrankung haben (p = 0,2), dann kann sich keine symmetrische Verteilung ergeben, wie Du in b) dargestellt hast - eine solche würde sich für eine Einzelwahrscheinlichkeit von p = 0,5 (siehe Aufgabe c) ergeben. 

 

Folgende Werte sollten richtig sein:

a)

P(X=0) = (5 über 0) * 0,2⁰ * 0,8⁵ = 1 * 1 * 0,32768 = 32,768%

P(X=1) = (5 über 1) * 0,2¹ * 0,8⁴ = 5 * 0,2 * 0,4096 = 40,96%

P(X=2) = (5 über 2) * 0,2² * 0,8³ = 10 * 0,04 * 0,512 = 20,48%

P(X=3) = (5 über 3) * 0,2³ * 0,8² = 10 * 0,008 * 0,64 = 5,12%

P(X=4) = (5 über 4) * 0,2⁴ * 0,8¹ = 5 * 0,0016 * 0,8 = 0,64%

P(X=5) = (5 über 5) * 0,2⁵ * 0,8⁰ = 1 * 0,00032 * 1 = 0,032%

 

Σ = 100%

 

Besten Gruß