Aufgabe:
Ein letztes Mal sollen Sie sich mit den Hämatokritwerten der 10 männlichen Patienten beschäftigen.
| Hämatokrit \( \mathrm{h}_{i}[\%] \) | 36 | 40 | 38 | 55 | 45 | 52 | 50 | 48 | 43 | 43 |
(a) Wir wollen annehmen, dass die den gemessenen Werten zu Grunde liegend Verteilung einer Normalverteilung entspricht. Schätzen Sie \( \mu \) und \( \sigma \) dieser Verteilung mit den Ihnen zur Verfügung stehenden Werkzeugen ab.
(b) Skizzieren Sie eine Normalverteilung mit den abgeschätzten Parametern.
(c) Wie Sie in der Vorlesung gelernt haben, sind Parameterschätzungen fehlerbehaftet. Tragen Sie in Ihre Skizze ein, in welchem Intervall um den geschätzten Wert \( \mu \) tatsächlich liegt. Das Konfidenzniveau liege bei 0,95 .
(d) Führen Sie für die gemessenen Werte eine z-Transformation durch und tragen Sie die so berechneten z-Werte in eine von Ihnen gezeichnete Standardormalverteilung ein.
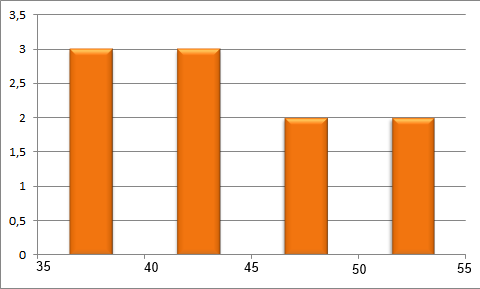
(e) Vergleichen Sie die von ihnen abgeschätzte Normalverteilung mit dem Histogramm aus Übung 1 Aufgabe 3 d. Ist die Annahme die Hämatokritwerte seien normalverteilt gerechtfertigt?
Meine Lösungsvorschläge:
Lösungen aus der 1.Übung:
\( \bar{h}=45 \)
\( \tilde{h}=44 \)
\( V \equiv H=h_{\max }-h_{\min }=19 \)
\( X \sim N\left(\mu, \sigma^{2}\right) \)
\( f(x)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}} \)
Normalverteilung hat Glockenform →Gau\betasche Glockenkurve
Maximalpunkt der Dichte: \( \mu \epsilon(-\infty,+\infty) \) Parameter \( \sigma^{2} \) mit \( \sigma>0 \) (Kurvenbreite) Wendepunkte: \( x_{W_{i}}=\mu-\sigma \) und \( x_{W_{2}}=\mu-\sigma \)
Erwartungswert: \( E(X)=\mu \) Varianz; \( D^{2}(X)=\sigma^{2} \)
Festlegung:
\( E(X)=45 \)
\( D^{2}(X)=38,44 \) [Varianz aus den 10 Werten; \( \left.s^{2}=38,44 \rightarrow s=6,20\right] \)