Was ist die beste Strategie für das hier beschriebene Kartenspiel?

Question

falls es so ein Thema schon gibt, tut es mir leid, aber die Suchfunktion konnte mir nicht helfen.

Ich suche nach der besten Strategie (stochastisch gesehen) für ein bestimmtes Kartenspiel. Auf der Seite dshini.net gibt es das Spiel "Dshinzilla". Die Regeln sind folgende:

• Es gibt 10 Karten.
• Man muss nacheinander sechs Dshini-Karten (also "gute" Karten) aufdecken.
• Findet man eine Dshinzilla-Karte (also eine "böse"), hat man verloren und muss von vorne anfangen.

Ich weiß leider nicht, wie viele Dshinzilla-Karten es gibt, gehe aber davon aus, dass es vier sind. Die Frage ist nun: Ist es sinnvoller, sich eine Kartenfolge auszusuchen und die immer wieder zu klicken, bis sie klappt, oder sollte man ohne Strategie einfach "wild in die Gegend" klicken? Bei welcher Vorgehensweise ist die Gewinnwahrscheinlichkeit höher? Kann man das stochastisch irgendwie berechnen?

Schon mal vielen Dank fürs Lesen und für alle Antworten, die vielleicht auftauchen. ;)

Comments

Ist das eine reales Kartenspiel oder ein virtuelles , im  zweiten fall  ist es lernendes? , in dem Fall gewinnt statistisch gesehen immer der Rechner ab einen gewissen Zeitpunkt!

Answer 1

Du kannst dir vorstellen, dass du jeweils auch bei Abbruch eigentlich 6 Karten gezogen hast. 'gute' und 'schlechte'. Wenn man annimmt, dass da zwischendrinn fair gemischt wird und eine Karte, die gezogen wurde, nicht nochmals kommen kann,

ist die Wahrscheinlichkeit, dass man die 6 'guten' Karten erwischt, bei jedem Spielbeginn wieder gleichgross. Sie ist auch nicht davon abhängig, in welcher Reihenfolge die 'guten' Karten aufgedeckt werden.

Zudem sollte bei einem sog. fairen Spiel jede Möglichkeit 6 bestimmte Karten zu erwischen gleich wahrscheinlich sein. (sog. 'Ziehen mit einem Griff')

Man kann sie berechnen aus der Formel

Wahrscheinlichkeit = (Anzahl günstige Fälle) / (Anzahl mögliche Fälle)

Die 'Fälle' sind sog. gleichwahrscheinliche Elementarereignisse. 

 

Es gibt 

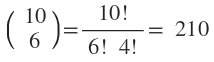
mögliche Fälle bei Ziehungen mit einem Griff.

Und

es gibt genau einen günstigen Fall, 'die richtigen 6 Karten' aufzudecken.

Die Gewinnwahrscheinlichkeit wäre deshalb 1 / 210 ≈ 0.00476 = 0.476%

Comments

Akelei hat natürlich recht. Gegen Computer verliert man auf die Dauer eh.