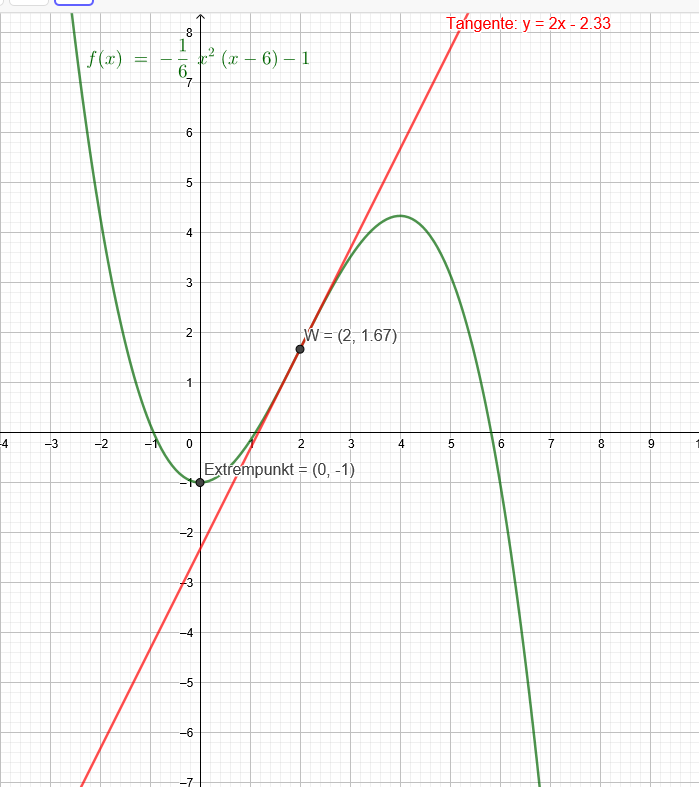
Lösung, falls keine Lösungsvorgaben existieren:
"Der Punkt P(0|-1) ist ein Extrempunkt; an der Stelle x=2 liegt ein Wendepunkt mit der Tangentensteigung von 2."
Verschoben um eine Einheit nach oben:
1.)P´(0|0) doppelte Nullstelle
p(x)=a*x^2*(x-N)=a*x^3-a*N*x^2
p´(x)=3ax^2-2aNx
p´(2)=3a*4-2aN*2
2.)12a-4aN=2 → 6a-2aN=1
p´´(x)=6ax-2aN
p´´(2)=6a*2-2aN
3.) 6a-aN=0
2.)-3.) -a N=1 in 3.) 6a+1=0 → a=-\( \frac{1}{6} \) in 2.)-3.) \( \frac{1}{6} \) N=1→N=6
p(x)=-\( \frac{1}{6} \) *x^2*(x-6)
Und eine Einheit nach unten:
f(x)=-\( \frac{1}{6} \) *x^2*(x-6)-1