Gibt es noch mehr Möglichkeiten, die binomischen Formeln zu zerlegen?

Question

also (a+b)^2 = a^2 + 2ab + b^2. Das kann man in R^2 ja auch visualisieren. Genauso wie man (a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 in R^3 visualisieren kann. Da stellt sich mir die Frage, ob man diese Formeln auch anders auflösen könnte? Z.B. als Flächeninhalte von Dreiecken, oder (näherungsweise! Weil Quadratur des Kreises ja nicht möglich ist) als Flächeninhalt eines Kreises. Oder als Flächeninhalt von Parallelolgrammen oder ähnliches. Geht das? Oder gibt es nur diese eine Möglichkeit, als Quadrate und Quadern?

Danke,

Thilo

Answer 1

Am Dreieck geht es relativ einfach.

Die Flächeninhaltsformel eines rechtwinkligen, gleichschenkligen Dreiecks mit dem Schenkel a ist

A = a²/2

Verlängert man die Seite um b, so ist der neue Flächeninhalt

A* = (a+b)²/2

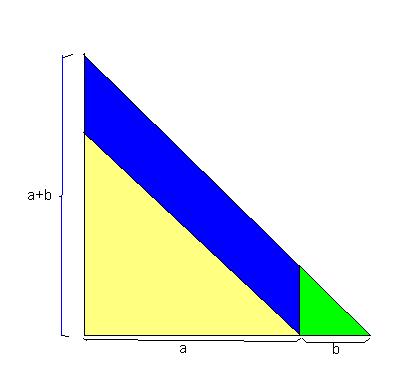
Zeichnet man sich das ganze auf, so erkennt man, dass sich das vergrößerte Dreieck zusammensetzen lässt aus einem Dreieck der Seitenlänge a, einem Dreieck der Seitenlänge b und einem Parallelogramm mit der Seitenlänge b und der Höhe a.

=> A* = a²/2 + b²/2 + a*b = 1/2* (a²+2ab+b²)

=> (a+b)² = a²+2ab+b²

 

Skizze:

Mit Parallelogrammen könnte man es nochmal ausprobieren, mit Kreisen halte ich es nach ein bisschen rumprobieren für unmöglich.

Comments

Danke, ich meinte aber eigentlich, ob es noch mehr Möglichkeiten für die Darstellung a^2 + 2ab + b^2 gibt, die nicht sofort ersichtlich sind. Also so etwas (Achtung, nur ein (falsches) Beispiel) (a+b)^2 = sin(a)*(2b)^2 oder so ähnlich ^^ Oder mit dem Modulo oder so etwas.