Die 3 Extrema bilden ein Dreieck. Berechnen Sie die Innenwinkel!

Question

F(x) = (1/4)x^4 - 2x^2

Hilfe wie berechne ich die Innenwinkel!

Answer 1

F ( x ) = (1/4) * x⁴ - 2 * x²

f ´( x ) = 4/4 * x^3 - 4 * x
x^3 - 4 * x = 0
x * ( x^2 - 4 ) = 0  => x = 0
x^2 - 4 = 0
x^2 = 4
x = 2
x = -2

f ( 0 ) 0
f ( 2 ) = ( 1/4 ) * 16 - 2 * 4
f ( 2 ) = -4

Die Funktion ist achsensymmetrisch bezogen auf die
y-Achse
Die Koordinaten der 3 Punkte sind
( -2 | -4 ) ( 0 | 0 ) ( 2  |- 4 )

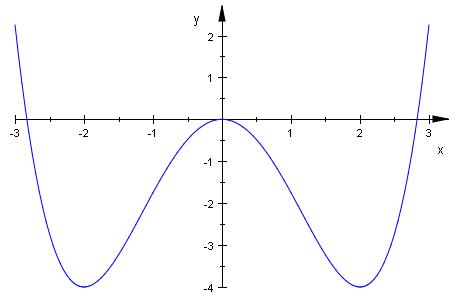
Der Winkel vom Punkt ( 0 | 0 ) zu einem der beiden anderen Punkte ist
( -4 - 0 ) /  ( 2 - 0 ) = 2
arctan ( 2 ) = 63.43 °

Der Winkel oben ist 2 * 63.43 ° = 126.86 °
Schafft du die anderen beiden Winkel allein ?

mfg Georg

Comments

warum bitte den winkel 2x 63,43??

---

Dein Dreieck besteht aus den Verbindungslinien der Extrempunkte.

Die Hälfte des Dreiecks wäre
( 0  | 0 )  ( 2  [ -4 ) ( 0 | -4 )
Ein rechtwinkliges Dreieck.
Der Winkel oben wäre = Gegenkatethe / Ankatethe
Winkel = 2 / 4 = 26.56 °.
Also Korrektur
26.56 ° * 2 = 53.12 °
Sonst zeichne das Ganze einmal im selben Maßstab auf.