f(x) = x³-5x+1
Als erstes habe ich geprüft, ob es achsensymmetrisch ist
f(5) = 5³-5*5+1 = 101
f(-5) = (-5)³-5*(-5)+1 = -99
101 ≠ 99 genügt schon: Nicht symmetrisch bezüglich y-Achse.
Es ist also nicht Achsensymmetrisch.
Bis hier hin ist alles richtig.
|101| ≠ |99| bedeutet, dass keine Symmetrie bezüglich (0/0) vorliegt.
Polynome sind genau dann symmetrisch bezüglich (0/0), wenn nur ungerade Potenzen von x vorkommen.
Der Summand +1 zerstört hier diese Symmetrie. Grund + 1 = 1*x^0 und 0 ist gerade.
Also:
g(x) = x^3 - 5x ist punktsymmetrisch bezüglich (0/0)
f(x) = x^3 - 5x +1 ist um 1 in y-Richtung verschoben und deshalb punktsymmetrisch bezüglich (0/1)
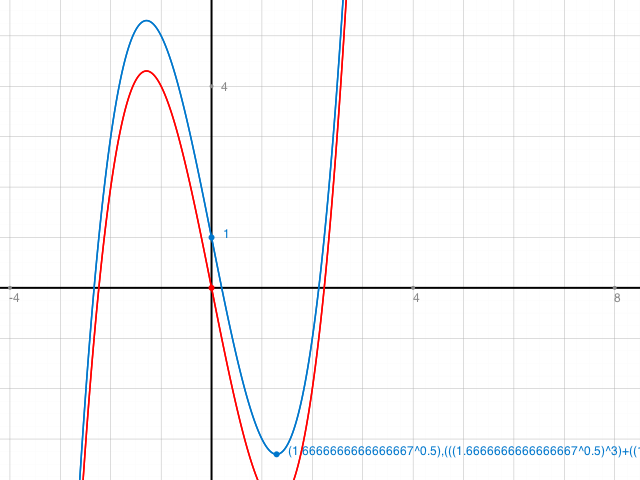
Hier die Graphen von f und g: