f(x)= 1/8 * (x^2 - 4x) auf der x-Achse zweimal schneidet. f und g stehen im Urspung senkrecht aufeinander
a.) WIe lautet die Gleichung von g
b.) Berechne den Inhalt der eingeschlossenen Flächen
f(x) hat die Nullstellen bei
f(x) = 0
x^2 - 4x = x(x - 4) = 0
x1 = 0 und x2 = 4
f(x) hat im Ursprung die Steigung
f'(0) = x/4 - 1/2 = -1/2
Senkrecht zur Steigung m ist die Steigung -1/m. Senkrecht zur Steigung -1/2 ist also die Steigung 2.
Damit kann ich mein Polynom versuchen aufzustellen
g(x) = ax^3 + bx <--- Punktsymmetrisch zum Ursprung bedeutet nur ungerade Potenzen von x
g(0) = 0 <--- Immer erfüllt da Punktsymmetrisch zum Ursprung
g(4) = 0
64·a + 4·b = 0
g'(0) = 2
b = 2
Die Lösung ist hier a = - 1/8 ∧ b = 2
f(x)= 1/8 * (x^2 - 4x) = x^2/8 - x/2
g(x) = -x^3/8 + 2x
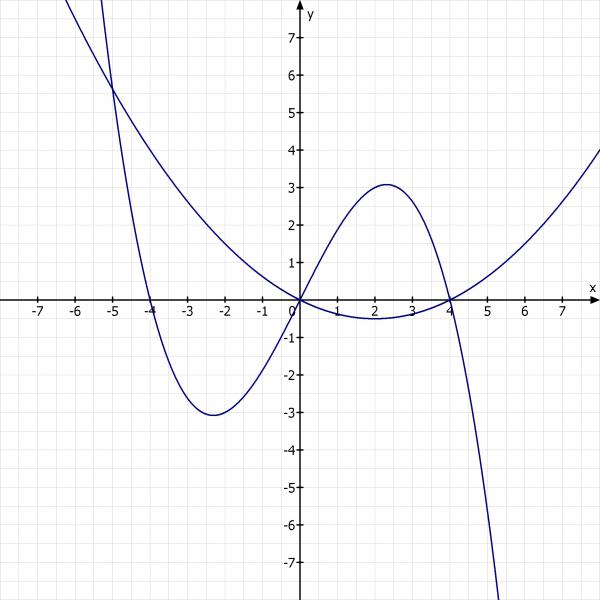
Skizze: