Mathe Steckbriefaufgabe 3. Grades

Question

Der Graph einer ganzrationalen Funktion dritten Grades verläuft durch P(0/-5) und Q(1/0) und er berührt die x-achse im Punkt R (5/0)

kann mir einer helfen ??

Answer 1

Hi,

f(0) = -5  (P)

f(1) = 0   (Q)

f(5) = 0    (R)

f'(5) = 0    (berührt die x-Achse, also tangiert)

Es ergibt sich

d = -5

a + b + c + d = 0

125a + 25b + 5c + d = 0

75a + 10b + c = 0

Und damit: f(x) = 0,2x^3 - 2,2x^2 + 7,5x - 5

Grüße

Answer 2

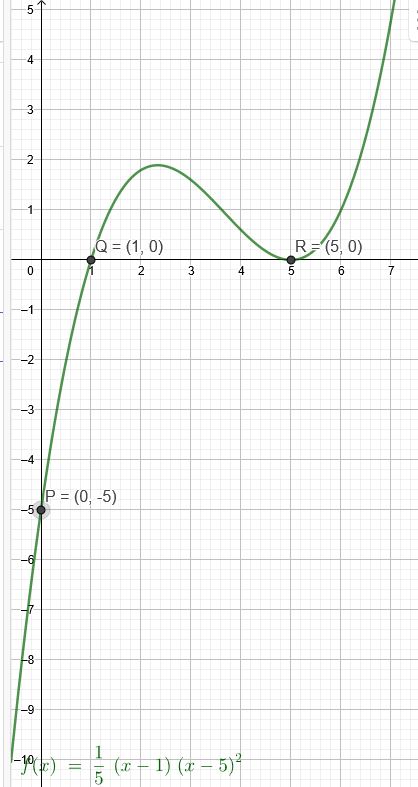
"Der Graph einer ganzrationalen Funktion dritten Grades verläuft durch P(0|-5) und Q(1|0), und er berührt die x-achse im Punkt R (5|0)"

einfache Nullstelle \(Q(1|0)\)   doppelte Nullstelle \(R (5|0)\) waagerechte Tangente

\(f(x)=a*(x-1)*(x-5)^2\)

\(P(0|-5)\)

\(f(0)=a*(0-1)*(0-5)^2=-25a\)           \(-25a=-5\)         \(a=\frac{1}{5}\)

\(f(x)=\frac{1}{5}*(x-1)*(x-5)^2\)