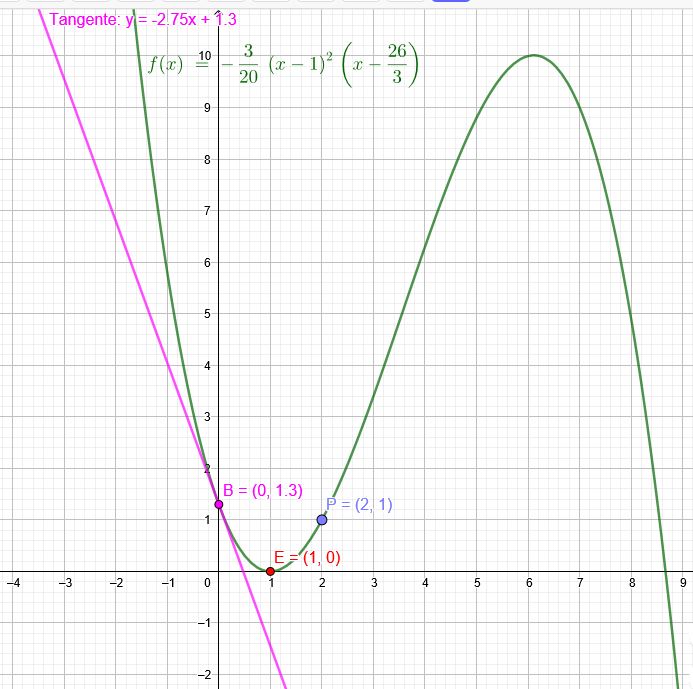
NST \(x = \red{1}\)
Tief - oder Hochpunkt \(x = \red{1}\)
beim Schnittpunkt mit der y - Achse Steigung \(m= \blue{- 2,75}\)
P\((2|1)\)
\(f(x)=a(x- \red{1})^2(x-N)\)
P\((2|1)\):
\(f(2)=a(2- \red{1})^2(2-N)=a(2-N)=1\) → \(a=\frac{1}{2-N}\)
\(f(x)=\frac{1}{2-N}[(x- \red{1})^2(x-N)]\)
\(f'(x)=\frac{1}{2-N}[2(x- 1)(x-N)+(x- 1)^2]\)
\(f'(0)=\frac{1}{2-N}[2(0- 1)(0-N)+(0- 1)^2]=\frac{1}{2-N}[2N+1]\)
\(\frac{1}{2-N}[2N+1]= \blue{- 2,75}\)
\(\frac{2N+1}{N-2}= 2,75\) \(N= \frac{26}{3} \) \(a=\frac{1}{2-\frac{26}{3} }=-\frac{3}{20}\)
\(f(x)=-\frac{3}{20}(x- 1)^2(x-\frac{26}{3})\)