Du möchtest wahrscheinlich wissen, wie man vorgeht, wenn man so eine Aufgabe bekommt:
Bestimmen Sie eine Gleichung der Geraden g, die durch die Punkte Q(2 | 5 | 1) und R(3 | 2 | 2) verläuft.
1. Schritt: Du wählst einen der Punkte als Stützvektor. Ich nehme jetzt z.B. Q als Stützvektor:
Das heißt \( \begin{pmatrix} 2\\5\\1 \end{pmatrix} \) ist unser Stützvektor.
2. Schritt: Du berechnest den Richtungsvektor, indem du den Stützvektor von dem 2. Punkt P subtrahierst.
Das heißt: R-Q=(3-2 | 2-5 | 2-1) = (1 | -3 | 1)
Also ist unser Richtungsvektor:\( \begin{pmatrix} 1\\-3\\1 \end{pmatrix} \)
3. Schritt: Aufstellen der Geradengleichung mit Stütz- und Richtungsvektor:
\( g: \vec{x} = \begin{pmatrix} 2\\5\\1 \end{pmatrix} + t · \begin{pmatrix} 1\\-3\\1 \end{pmatrix} \)
Ich hoffe, dass du das jetzt vertsehen kannst.
Vielleicht hilft dir diese Abbildung, damit du dir den Sachverhalt bildlich vorstellen kannst:
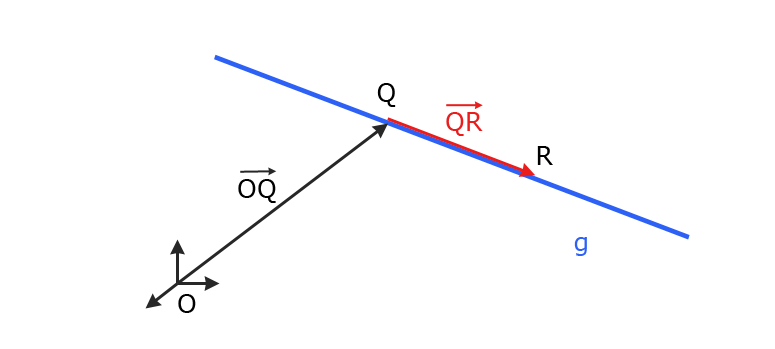
Nutze auch den Geoknecht 3D und erstelle eigene Vektoren!