Aufgabe 361c):
Bestimme den Grad der Polynomenfunktion aus den gegebenen Eigenschaften. Ermittle den Funktionsterm.
Der Graph der Polynomfunktion hat genau einen Wendepunkt an der Stelle x=-1
f''(-1) = 0
, schneidet die x-Achse an den Stellen x=-2
f(-2) = 0
und x=1
f(1) = 0
und geht durch den Punkt (0/-2).
f(0) = -2
Ich hab keinen Plan wie ich das herausfinden soll.
Erstmal haben wir hier 3 Bedingungen und damit eine Funktion 3. Grades mit 4 Parametern.
f(x) = ax^3 + bx^2 + cx + d
f'(x) = 3ax^2 + 2bx + c
f''(x) = 6ax + 2b
Ich setzte jetzt die obigen Bedingungen in ein Gleichungssystem um
f''(-1) = 0
2·b - 6·a = 0
f(-2) = 0
- 8·a + 4·b - 2·c + d = 0
f(1) = 0
a + b + c + d = 0
f(0) = -2
d = -2
Wir lösen das Gleichungssystem mit z.B. mit dem Additionsverfahren und erhalten die Lösung
a = 0.5 ∧ b = 1.5 ∧ c = 0 ∧ d = -2
Die Funktion lautet daher
f(x) = 0.5x^3 + 1.5x^2 - 2
Ich mache jetzt noch eine Skizze der Funktion
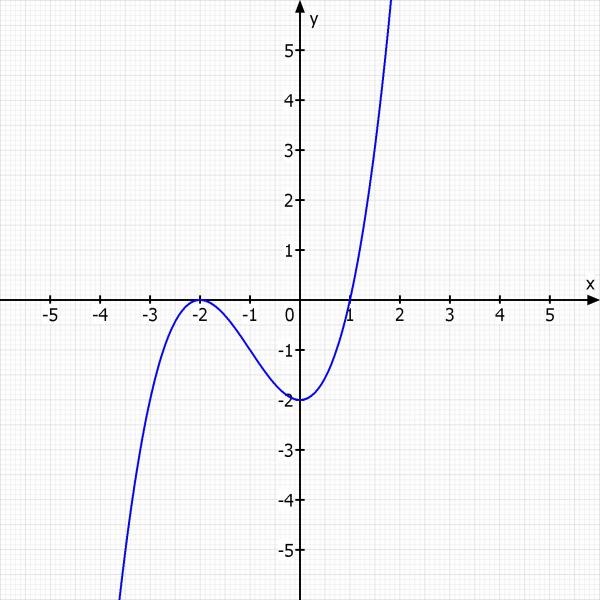
Eine Schritt für Schritt Lösung des Gleichungssystems bekommst Du z.B. bei Wolfram Alpha, wenn du damit noch Schwierigkeiten hast.
https://www.wolframalpha.com/input/?i=2b-6a%3D0%2C-8a%2B4b-2c%2Bd%3D0%2Ca%2Bb%2Bc%2Bd%3D0%2Cd%3D-2