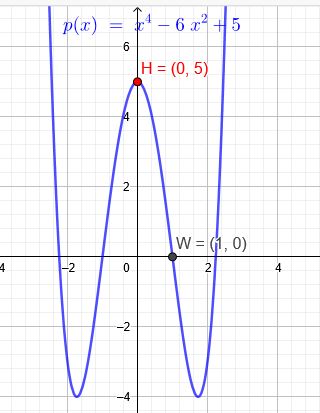
Der Graph einer Funktion vierten Grades verläuft symmetrisch zur Ordinate und hat in H( 0 | 5 ) ein Maximum und in W( 1 | 0 ) einen Wendepunkt.
Verschieben um 5 Einheiten nach unten:
H´( 0 | 0)
\(f(x)=ax^2(x-N)(x+N)=ax^2(x^2-N^2)=a(x^4 - N^2 x^2)\)
W( 1 | 0 ) →. W´( 1 | -5 )
\(f(1)=a(1- N^2 )=-5\)
\(a=\frac{5}{N^2-1}\)
\(f(x)=\frac{5}{N^2-1}(x^4 - N^2 x^2)\)
W´( 1 | ... ):
\(f'(x)=\frac{5}{N^2-1}(4x^3 - 2N^2 x)\)
\(f''(x)=\frac{5}{N^2-1}(12x^2 - 2N^2 )\)
\(f''(1)=\frac{5}{N^2-1}(12 - 2N^2 )=0\)
\(N^2=6\)
\(a=1\)
\(f(x)=x^4 - 6 x^2\)
Verschieben um 5 Einheiten nach oben:
\(p(x)=x^4 - 6 x^2+5\)