Im Inneren des Würfels befindet sich eine Kugel. Schneidet sich die Kugel mit der von A, B, C aufgespannten Ebene?

Question

Aufgabe:

Sei ein Würfel mit Kantenlänge 4 gegeben, \( A \) und \( C \) seien Kantenmittelpunkte und \( B \) liege in der Höhe 3 über dem Boden des Würfels. Das Koordinatensystem sei so gewählt, dass der Nullpunkt das Zentrum des Würfels ist und \( B=(2,-2,1) \).

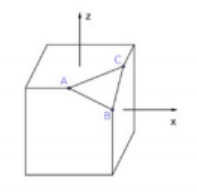
a) Berechnen Sie den Winkel \( \beta \).

b) Im Inneren des Würfels befindet sich eine Kugel, die alle Seitenflächen des Würfels berührt. Schneidet sich die Kugel mit der von \( A, B, C \) aufgespannten Ebene?

c) Verlässt ein Strahl, der vom Zentrum des Würfels aus in Richtung \( v=(1,-1,2)^{t} \) geht, den Würfel durch die Fläche des Dreiecks \( A B C \)?

Answer 1

du musst hier mit der Vektorrechnung arbeiten.

Erstmal würde ich einen Ortsvektor zu B und dann die Spannvektoren AB und CB bestimmen, wodurch du eine Ebenengleichung angeben kannst. dann kannst du mit dem Skalarprodukt (entsprechend umgestellt) den Winkel am Punkt B bestimmen.

Mehr fällt mir leider momentan auch nicht ein...