Oberfläche eines Würfels und Kugel

Question

Kann mir bitte einer erklären wie ich diese Aufgabe Lösen

Vergleiche die Oberfläche eines Würfels mit 1m Kantenlänge und die Oberfläche einer Kugel mit dem gleichen Volumen

Answer 1

Oberflächeninhalt eines Würfels=6*a²=6m²

Volumen eines Würfels=a*a*a=a³=1m³

Zur Kugel:

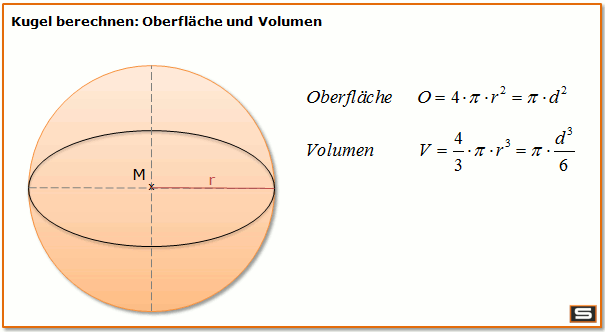
Volumen einer Kugel: Schon angegeben 1m³=4/3π*r³ Wir stellen nach r um, da wir das für die Oberfläche brauchen werden.

3/4:π=r³=0,238m  Nun die 3. Wurzel

-->0,62m ist der Radius

Die Oberfläche soll verglichen werden, daher rechnen wir ihn aus

O=4πr²=4,836m²

Das Volumen ist zwar gleich, der Oberflächeninhalt ist jedoch kleiner als bei dem Würfel.

Bei Unklarheiten fragen.

Answer 2

Vergleiche die Oberfläche eines Würfels mit 1m Kantenlänge und die Oberfläche einer Kugel mit dem gleichen Volumen

6·(v^{1/3})^2 / (4·pi·(6^{1/3}·v^{1/3}/(2·pi^{1/3}))^2) = (6/pi)^{1/3} = 1.2407

Die Würfeloberfläche ist (6/pi)^{1/3} mal so groß wie die Kugeloberfläche. Also ca. 24.07% größer

Comments

Jap, kann ich bestätigen, 6:4,836=1,24069 also 24,07 größer