1.) Terassenpunkt und Sattelpunkt meint das selbe, oder?
2.) Wenn die Funktion durch 0;0 verläuft, dann ist sie "punktsymmetrisch", also hat nur ungerade Exponenten, richtig? Die Formulierung "der Terassenpunkt (0;0" ändert nichts oder? Oder kommt es auch darauf an, an welchem Punkt die Funktion durch den Ursprung geht, damit sie "punktsymmetrisch" ist?
1.)Terassenpunkt und Sattelpunkt meint dasselbe, noch ein Synonym ist der Horizontalwendepunkt.
Dies tritt ein, wenn durch einsetzen von x=0 in die Gleichungen f(x) f'(x) diese auch = 0 werden, f'''(x) jedoch ≠ 0 ist.
2.) Wenn sie durch 0|0 geht ist sie nicht unbedingt punktsymmetrisch. Es besteht auch die Möglichkeit gar keiner Symmetrie oder der Achsensymmetrie. Dabei sind ungerade Exponenten ein Anzeichen für Punktsymmetrie und dementsprechend gerade Exponenten für Achsensymmetrie.
Noch klarer kann das Einsetzen von f(-x)=f(x) sein. Wenn diese beiden dasselbe sind, liegt eine Achsensymmetrie vor.
-f(x)=f(-x) impliziert Punktsymmetrie
Der Ursprungspunkt ist daher unerheblich, da ja auch eine Verschiebung auf der y bzw. x Achse vorliegen könnte.
Bei weiteren unklaren Sachverhalten gerne melden
Gruß Luis
PS:
Achsensymmetrische Funktion
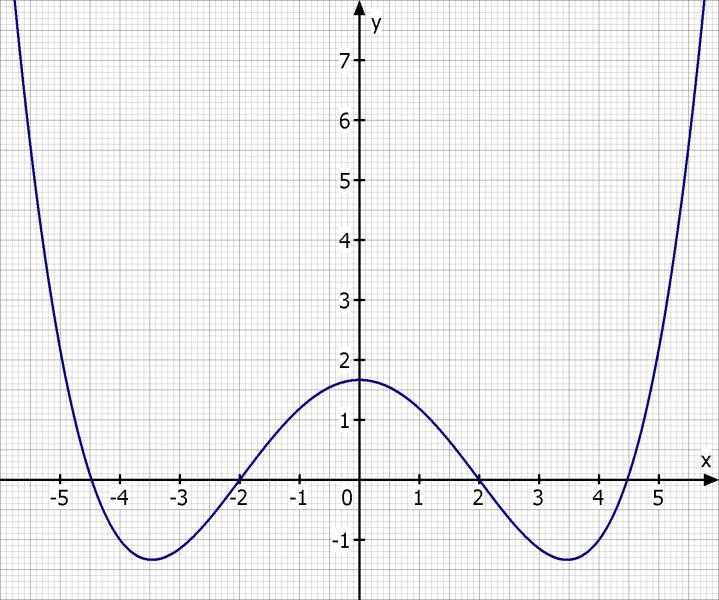
Punktsymmetrische Funktion (zentralsymmetrisch)
