Aufgabe 1:
Bei einem Forschungsprojekt über Rohrpost-Systeme wird eine zylinderförmige Transportkapsel in einer \( 100 \mathrm{~m} \) langen geraden Röhre mit Druckluft hin und her bewegt. Die Geschwindigkeit der Kapsel wird während eines Testlaufs in Abhängigkeit von der Zeit aufgezeichnet. Die Funktion \( \mathrm{f} \) mit der Gleichung
\( f(t)=\frac{1}{12} t^{3}-\frac{4}{3} t^{2}+4 t=\frac{1}{12} t(t-4)(t-12), t \in \mathbb{R} \)
beschreibt diese Geschwindigkeit im Zeitintervall \( [0 ; 12] \).
(Mit Geschwindigkeit ist stets die Momentangeschwindigkeit gemeint.)
Dabei wird \( \mathrm{t} \) als Maßzahl zur Einheit \( 1 \mathrm{~s}, \mathrm{f}(\mathrm{t}) \) als Maßzahl zur Einheit \( 1 \mathrm{~m} / \mathrm{s} \) aufgefasst. Zum Zeitpunkt \( \mathrm{t}=0 \) ist die Kapsel in der Mitte der Röhre in der Position \( 0 \mathrm{~m} \) und setzt sich vorwärts in Bewegung. Das vordere Ende der Röhre entspricht der Position \( 50 \mathrm{~m} \), das rückwärtige Ende der Position \( -50 \mathrm{~m} \). Negative Werte der Geschwindigkeit entsprechen einer Rückwärtsbewegung der Kapsel.
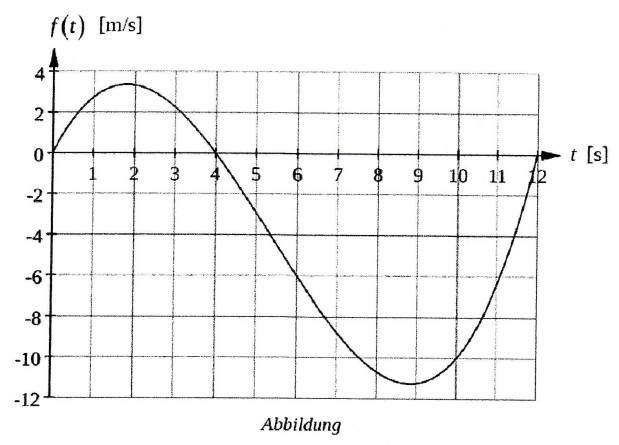
a)
1. Berechne den Funktionswert von fan der Stelle \( t=6 \) und interpretiere diesen Wert im Sachzusammenhang.
2. Gib die Zeiträume an, in denen sich die Kapsel vorwärts bzw. rückwärts bewegt.
b)
1. Bestimme den maximalen und den minimalen Wert der Geschwindigkeit der Kapsel im Zeitintervall \( [0 ; 12] . \)
2. Ermittle den minimalen Wert der Beschleunigung \( (= \) momentane Anderungsrate der Geschwindigkeit) der Kapsel im Zeitintervall \( [0 ; 12] \).
3. Interpretiere das negative Vorzeichen des Wertes aus 2. im Sachzusammenhang.
c)
1. Berechne \( F(t)=\int \limits_{0}^{t} f(u) d u \) und interpretiere \( F(t) \) im Sachzusammenhang.
2. Berechne, wo sich die Kapsel nach 12 Sekunden befindet.
3. Ermittle den Zeitpunkt, zu dem die Kapsel den Startpunkt wieder passiert.
4. Bestimme die mittlere Geschwindigkeit der Kapsel während der Vorwärtsbewegung.
d) Bei einem zweiten Testlauf wird die Geschwindigkeit der Kapsel im Zeitintervall \( [0 ; 12] \) durch die Funktion \( \mathrm{g} \) mit der Gleichung \( g(t)=a t, t \in \mathfrak{R} \) beschrieben, wobei der Parameter \( a \in \Re \) eine konstante Beschleunigung darstellt.
Untersuche, für welche Werte von a Zeitpunkte nach dem Start existieren, zu denen die Geschwindigkeit der Kapsel bei beiden Testläufen gleich ist.