Wie liegen die Graphen Kf und Kg zueinander?

Question

Halli :)

ich hab hier jede Menge Aufgaben, jedoch mit 2 komme ich einfach nicht weiter :/

a) f(x)=-x^4+2x^3 ; g(x)=0,5x^2

b) f(x)=-0,5(x^3-4x-2) ; g(x)=-4x-7

Man muss die ja gleichetzen,aber dabei komme ich durcheinender :(

Answer 1

Wie liegen die Graphen Kf und Kg zueinander?

Ja. Da musst du feststellen, wie oft sich die beiden Graphen schneiden.

Gleichsetzen der Funktionsgleichungen ist da die übliche Methode.

-x⁴+2x³ =0,5x² 

0 = x^4 - 3x^3 + 0.5x^2

0 = x^2 (x^2 - 3x + 0.5)

x1 = x2 = 0 doppelte Lösung. Daher in x=0 Berührung der beiden Graphen.

x^2 - 3x + 0.5 = 0

x3,4 = 1/2 (3 ±√(9 - 2)) = 1/2 ( 3± √7)

an diesen beiden Stellen schneiden sich die Graphen.

Insgesamt haben die Graphen von a) 3 gemeinsame Punkte. 

b)

-0,5(x³-4x-2) =-4x-7 

0 = 0.5x^3 - 2x - 1 - 4x - 7

0 = 0.5 x^3 - 6x - 7

0 = x^3 - 12x - 14 

x^3 = 12x + 14

y = x^3 wird auf jeden Fall im 1. Quadranten mal noch die Gerade  y = 12x + 14 schneiden, da die Steigung von y=x^3 im 1. Quadranten monoton von 0 bis unendlich steigt.

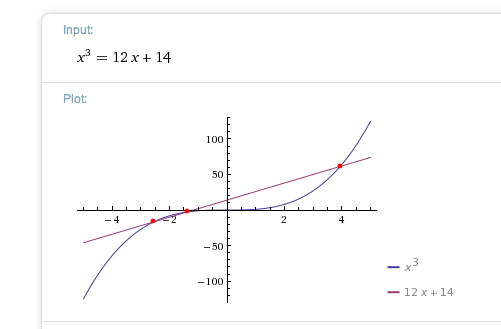
Es gibt gemäss Link noch 2 weitere Schnittstellen von f und g. 

Gegenseitige Lage: Die Graphen schneiden sich.