Thema Wirtschaftsmathematik und Produktionskosten.
Aufgabe:
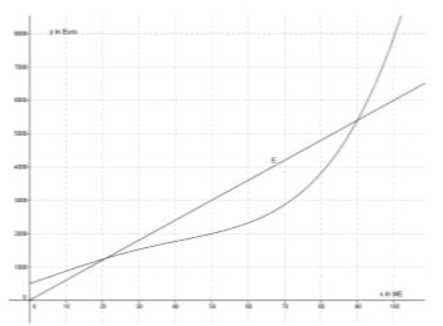
Die untenstehende Abbildung zeigt die Graphen der Kostenfunktion K und die Erlösfunktion E des Betriebes, wobei x die Anzahl der produzierten und verkauften Mengeneinheiten (ME) pro Tag ist. 1 ME entspricht einer Verpackungseinheit von 100 Stück. Pro Tag können höchstens 110 ME produziert werden.
Aufgabenstellung:
a)
Ermitteln Sie anhand der obigen Abbildung den Gewinnbereich, das sind jene Stückzahlen (1 ME = 100 Stück), für die der Betrieb Gewinn erzielt.
Beschreiben Sie, wie sich eine Senkung des Verkaufspreises auf den Verlauf des Graphen der Erlösfunktion \( E \) auswirkt und wie sich dadurch der Gewinnbereich verändert.
b)
Bestimmen Sie anhand der Abbildung die Fixkosten und den Verkaufspreis pro ME möglichst genau!
c)
Welche der nachstehenden Aussagen treffen für die in der Grafik abgebildeten Produktionskosten zu?
Kreuzen Sie die beiden zutreffenden Aussagen an.
▢ Bei degressivem Kostenverlauf gilt: \( K^{\prime}(x)<0 \)
▢ Bei progressivem Kostenverlauf gilt: \( K^{n \prime}(x)>0 \)
▢ Bei der Kostenkehre gilt: \( K^{\prime}(x)=0 \)
▢ Für alle \( x \) aus dem Definitionsbereich \( [0 ~ M E ; 110 M E] \) gilt: \( K^{\prime}(x)>0 \)
▢ Es gilt: \( K^{\prime}(50)>K^{\prime}(90) \)
Erklären Sie ausführlich, was die 1. und 2. Ableitung der Kostenfunktion an einer bestimmten Stelle, über den Verlauf des Graphen von \( K \) an dieser Stelle aussagen!
d)
Deuten Sie die Beziehung \( K^{\prime}(x)=E(x) \) geometrisch und ermitteln Sie anhand der nachstehenden Abbildung jene Produktionsmenge \( x \), für die das zutrifft.
Begründen Sie, warum der erzielte Gewinn bei dieser Produktionsmenge \( x_{1} \) am größten ist.