Aufgabe 1:
f(x)= 4*x -2/(2x)+4; Asymptoten: y-Achse x= 0 oder a(x) = -1/x; a(x) = 4*x + 4;
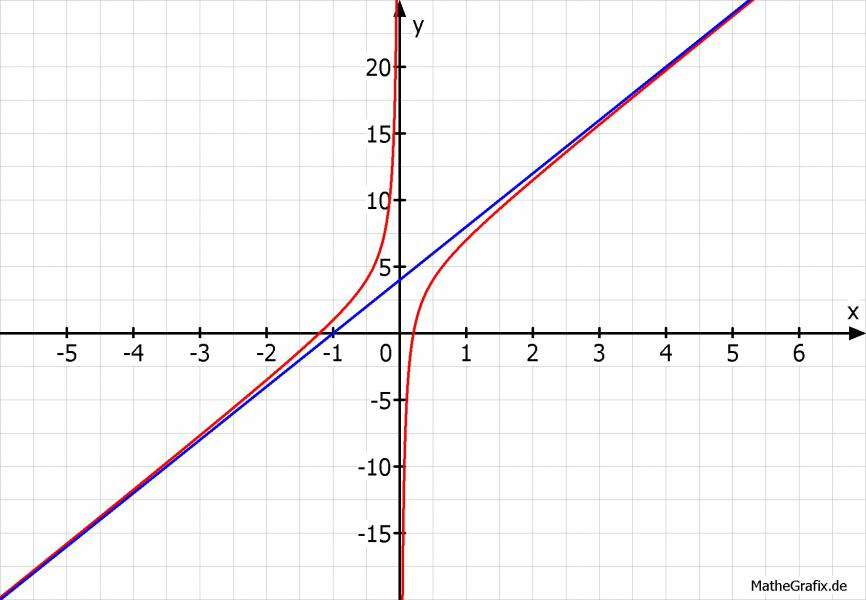
Aufgabe 2:
f(x)= 3*x - 6/x2-4; Asymptoten: y-Achse oder a(x) = - 6/x2, a(x) = 3*x - 4;
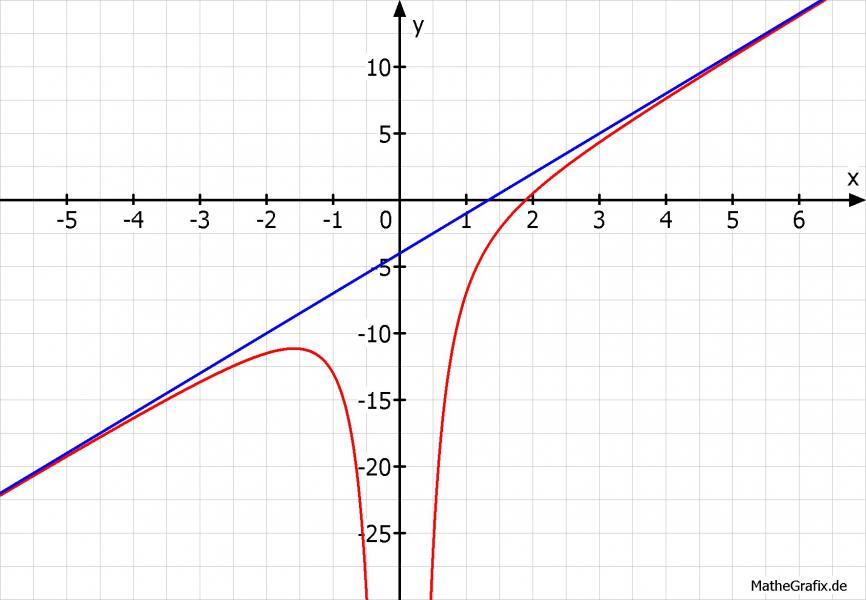
Aufgabe 3:
f(x)= 3*x^2+2*x+1/(2*x)+1; Asymptoten: für x→±0 a1(x) = 1/(2*x) oder y-Achse; für x→∞ a2(x) = 3*x^2; (Kurven-Asymptoten);
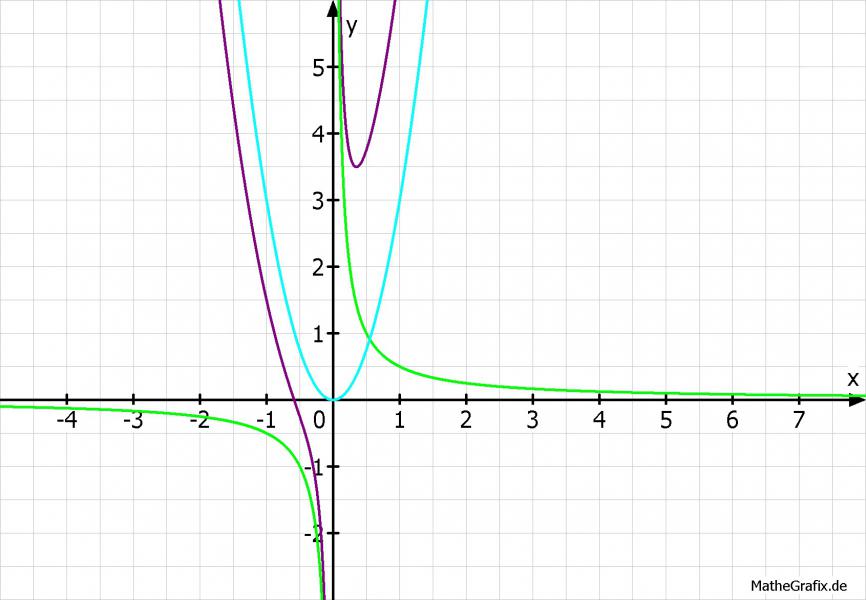
Aufgabe4:
f(x) = x^3-3*x + 2/x + 2; Asymptoten: für x→±0 a1(x) = 2/x oder y-Achse; für x→∞ a2(x) = x^3; (Kurven-Asymptoten);
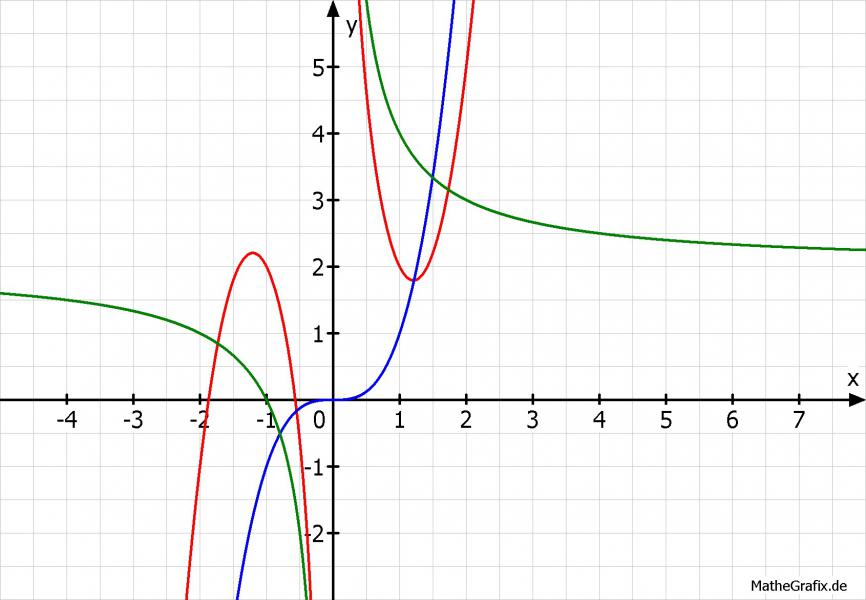
Bin mir bei den Gleichungen nicht ganz sicher, die hast Du leider nicht ganz eindeutig aufgeschrieben.
lg JR