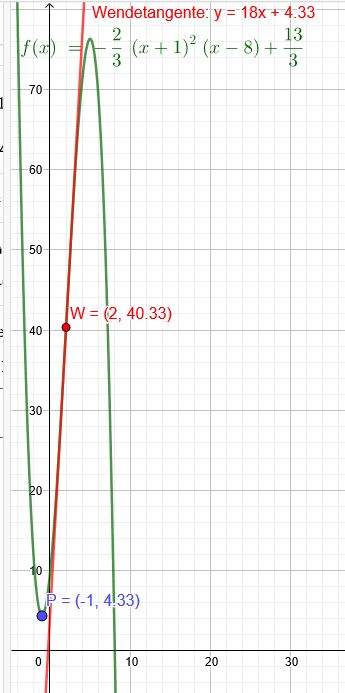
"Der Graph einer ganzrationalen Funktion dritten Grades hat in P(−1∣313 ) einen Tiefpunkt. An der Stelle x=2 liegt ein Wendepunkt mit einer Tangente vor, die Parallel zu der Geraden mit y=18x+3 verläuft."
Tiefpunkt P(−1∣313 ) →Tiefpunkt P´(−1∣0 ) doppelte Nullstelle
f(x)=a∗(x+1)2∗(x−N)
f´(x)=a∗[(2x+2)∗(x−N)+(x+1)2]
Wendestelle bei: x=2
f´´(x)=a∗[(2x−2N)+(2x+2)+2∗(x+1)]
f´´(x)=a∗[(2x−2N)+4x+4]
f´´(2)=a∗[(4−2N)+12]=0 N=8
f´(x)=a∗[(2x+2)∗(x−8)+(x+1)2]
Steigung Wendetangente m=18
f´(2)=a∗(−27)=18 a=−32
f(x)=−32∗(x+1)2∗(x−8)
p(x)=−32∗(x+1)2∗(x−8)+313