Ganzrationale Funktion dritten Grades aus Tiefpunkt und Wendepunkt bestimmen

Question

ich mache gerade meine Mathehausaufgaben und habe das Thema leider nicht wirklich verstanden.
Ich muss eine ganzrationale Funktion dritten Grades aus dem Tiefpunkt T(1|2) und dem Wendepunk (0|0) bestimmen, dazu wird gefragt, ob es möglich ist oder nicht.

Da es sich um eine ganzrationale Funktion dritten Grades handelt, lautet die allgemeine Funktionsgleichung:
f(x)=ax³+bx²+cx+d

Und die Ableitung:
f'(x)=3ax²+2bx+c

Jedoch komme ich nicht weiter, ich weiß noch nicht einmal wie ich anfangen soll.

Comments

f(0) = 0 -> d =0

f'(1) = 0
⇔ 3a + 2b + c = 0
⇔ c = - 3a - 2b

f(1) = a + b + c = 2

Answer 1

Eigentlich ist es nicht möglich, da sich bei einer Funktion 3. Grades der Tiefpunkt von der y-Koordinate unterhalb des Wendepunktes befinden sollte. Wir müssten also bei (1|2) ein Hochpunkt haben oder ein Tiefpunkt bei (1|-2). Ich wähle mal den Hochpunkt bei (1|2).

f(x) = a·x^3 + b·x^2 + c·x + d
f'(x) = 3·a·x^2 + 2·b·x + c
f''(x) = 6·a·x + 2·b

Hochpunkt (1|2)

f(1) = 2
a + b + c + d = 2

f'(1) = 0
3·a + 2·b + c = 0

Wendepunk (0|0)

f(0) = 0
d = 0

f''(0) = 0
2·b = 0

Das ganze ist ein Gleichungssystem von 4 Gleichungen mit 4 Unbekannten und das sollte lösbar sein.

a + b + c + d = 2
3·a + 2·b + c = 0
d = 0
b = 0

Wir setzen zunächst mal b und d in die anderen Gleichungen ein und können dann auch leicht a und b ausrechnen. Die Lösung finden wir mit a = -1 ∧ b = 0 ∧ c = 3 ∧ d = 0

f(x) = -x^3 + 3·x

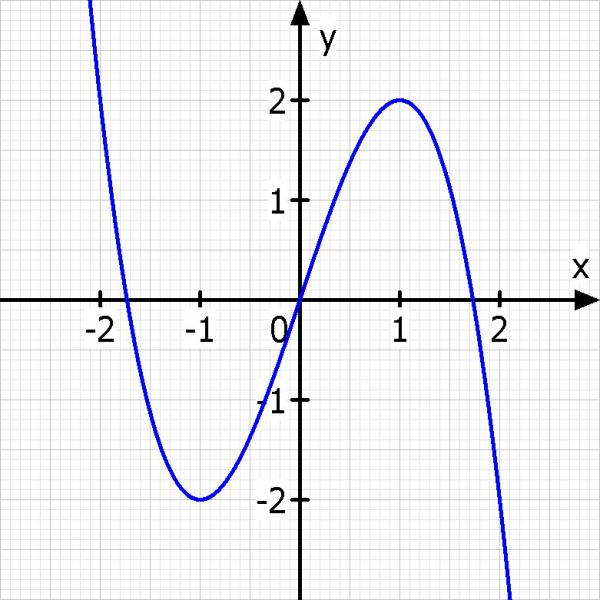
Skizze:

Comments

Hatte gerade ein ähnliches Problem und deine Antwort hat mir dann ein Licht aufgehen lassen. Wollte nur mal Danke sagen :D