Ermittlung der Funktionsgleichung durch die Punkte (1|2) und (3|7)

Question

Ich soll eine Funktionsgleichung aus zwei Punkten ermitteln.

Beispiel: A(1|2) und B(3|7)

Wie geht das?

Comments

Ähnliche Fragen mit ausführlichen Berechnungen:

• Funktionsgleichung aus 2 Punkten ermitteln?
• Funktionsgleichung bestimmen: Gerade geht durch 2 gegebene Punkte
• Funktionsgleichung anhand 2 gegebener Punkte
• Gleichung für eine Gerade finden
• Funktionsgleichung bestimmen: Gerade geht durch Punkte (3|4,5) und (-9|8,5)

Answer 1

Die allgemeine Form der Gleichung einer linearen Funktion lautet:

f(x) = ax+b

 

Setzt du nun diese beiden Punkte ein, dann erhältst du ein Gleichungssystem, aus dem du a und b bestimmen kannst:

f(1) = 2: a*1+b = 2

f(3) = 7: a*3 + b = 7

Ziehst du die erste von der zweiten Gleichung ab, so erhältst du:

a*3+b - (a*1+b) = 7-2

2a = 5 | :2

a = 2,5

 

Aus der ersten Gleichung lässt sich jetzt sehr einfach b bestimmen:

2,5*1 + b = 2 | -2,5

b = -0,5

 

Die Funktionsgleichung lautet also:

f(x) = 2,5x - 0,5

Answer 2

Annahme : es handelt sich um eine lineare Gleichung , da ist die  ist die Form

f(x)=bx+c         nun die beiden Punkte  einsetzen und man erhält zwei Gleichungen

f(2)=1*b+c    ⇒   2=b+c     ⇒2-b=c    dies unten einsetzen

f(7)=3b+c     ⇒    7=3b+(2-b)    ⇒  7=2b+2      5=2b     b=5/2 oder b=2,5

 wieder in die erst Gleichung einsetzen    2-2,5=c   ⇒c=-0,5

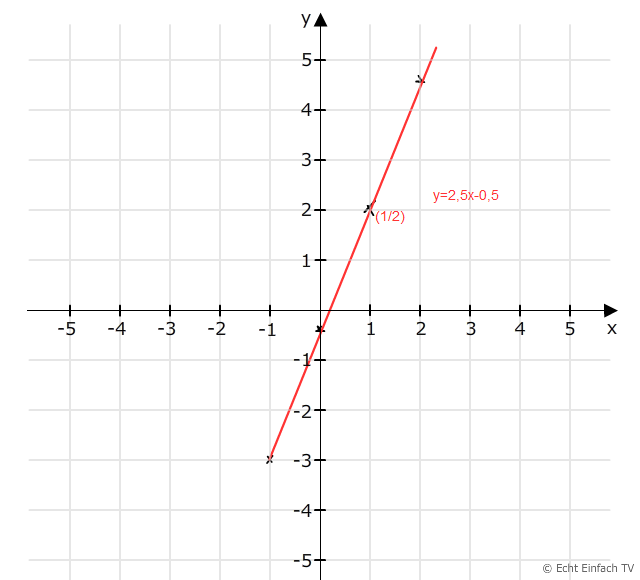
 also sieht die lineare Gleichung so aus

f(x)=2,5x-0,5      oder  f(x)=(5/2)*x-(1/2)

(Eine andere Lösungsverfahren  wäre das Additionverfahren, hier angewendet ist das Einsetzungsverfahren.)