Achtung: Dieser Dateityp ist nicht erlaubt. Mach eine ZIP-Datei daraus und lade diese hoch.
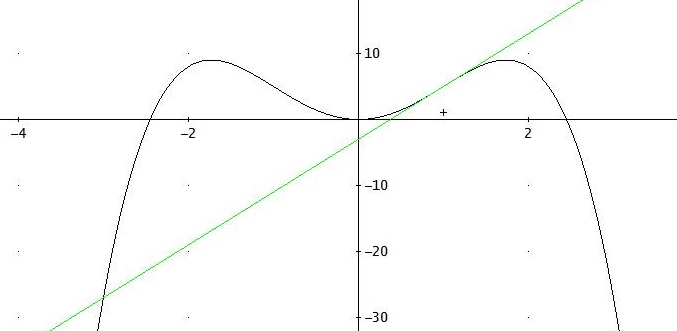
f (x)= 6x2 -x4 ; t(x) = 8x -3
Gleichsetzen:
6x2 -x4 = 8x -3
x4 - 6x2 + 8x - 3 = 0
Da die Tangente den Graph berührt, ist x = 1 eine mindestens doppelte Nullstelle.
Du kannst den Term x4 - 6x2 + 8x - 3 zweimal durch den zugehörigen Linearfaktor (x-1) dividieren (Polynomdivision) und ggf. die restlichen Nullstellen durch Nullsetzen des quadratischen Restterms bestimmen (pq-Formel)
Zur Kontrolle: nach der zweimaligen Polynomdivision erhältst du
x 2 + 2·x - 3 mit den Nullstellen x =1 und x = -3
(-3 | t(-3) ) = (-3 | f(-3) ) ist also der zweite Schnittpunkt