Funktion f(x): = e^{-x} - e^{-2x}. suche Nullstellen, horizontale Tangenten, Wendepunkte…

Question

Gegeben ist die Funktion...bestimmen von Nullstellen, h. Tangente, Wendepunkt etc.

!

Gegeben ist die Funktion f(x) = e^{-x} - e^{-2x}

a) Bestimmen Sie die Nullstellen, horizontalen Tangenten, Wendepunkte und das Verhalten im Unendlichen.

b) Der Graph schliesst mit der x-Achse im 1. Quadranten eine Fläche ein, die sich bis ins Unendliche erstreckt.

Wie gross ist der Flächeninhalt?

Answer 1

f(x) = e^{-x} - e^{- 2·x}
f'(x) = 2·e^{- 2·x} - e^{-x}
f''(x) = e^{-x} - 4·e^{- 2·x}
F(x) = 0.5·e^{- 2·x} - e^{-x}

Nullstellen f(x) = 0

e^{-x} - e^{- 2·x} = 0 | z = e^{-x}
z - z^2 = 0
z(1 - z) = 0
z = 0 --> x = -ln(0) = keine Lösung
z = 1 --> x = -ln(1) = 0

Horizontale Tangenten f'(x) = 0

2·e^{- 2·x} - e^{-x} = 0 | Lösen wie vorher über Substitution
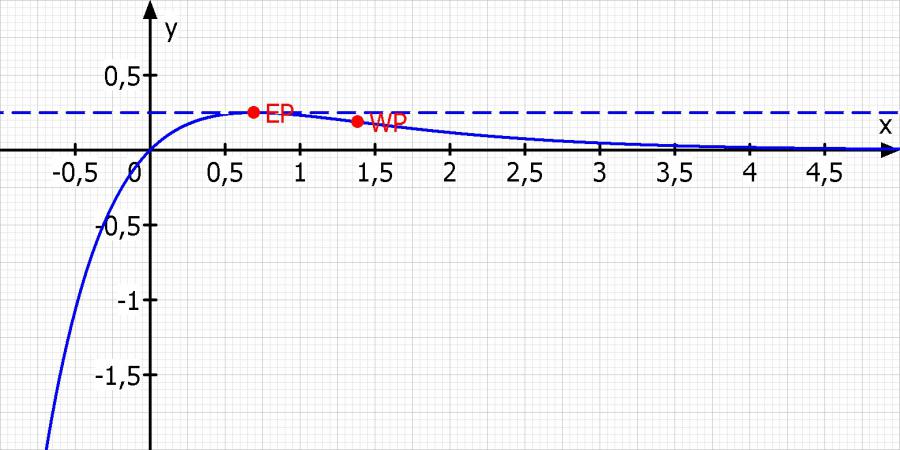
x = ln(2)

f(ln(2)) = 0.25

t(x) = 0.25

Wendepunkte f''(x) = 0

e^{-x} - 4·e^{- 2·x} = 0 | Auch hier wieder Lösen über Substitution
x = 2·ln(2)

f(2·ln(2)) = 3/16

WP(2·ln(2) | 3/16) = WP(1.386 | 0.1875)

lim _{x → -∞} f(x) = -∞
lim _{x → ∞} f(x) = 0

Fläche

F(∞) - F(0) = 0 - (-0.5) = 0.5

Skizze: