f(x) = -2x2 + 2x - 7
f '(x) = -4x + 2
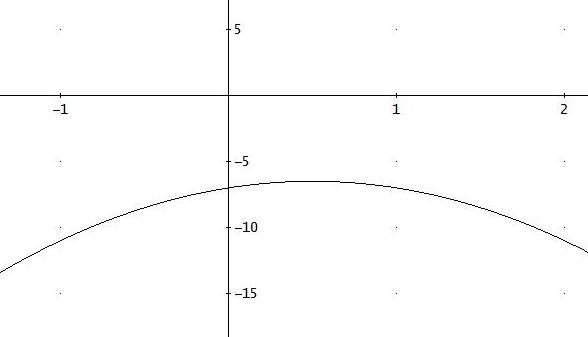
a) Nullstellen von f: -2x2 + 2x - 7= 0 hat keine Lösung → keine Nullstellen.
b) Scheitelpunkt: f ' ( xs ) = 0 ⇔ -4xs + 2 = 0 ⇔ xs = 1/2
f(1/2) = -13/2 → S( 1/2 | -13/2)
c) die Behauptungen sind richtig, weil alle x∈ℝ problemlos in f(x) eingesetzt werden können, und alle y-Werte bei dieser nach unten geöffneten Parabel ≤ -13/2 sind.
Gruß Wolfgang