Question

Berechnen Sie den Reihenwert der folgenden Reihe:

(a)

\( \sum \limits_{n=0}^{\infty} \sum \limits_{m=0}^{n}\left(\begin{array}{c}{n} \\ {m}\end{array}\right)(1 / 2)^{n+m} \)

Wie berechne ich den Reihenwert?

Kann mir das jemand zeigen, sodass ich die anderen Teilaufgaben lösen kann?

Comments

Hinweis: binomischer Lehrsatz.

---

https://www.mathelounge.de/291244/reihenwert-einer-reihe-berechnen-doppelsumme

Answer 1

Hi,
Für die innere Summe von $$ \sum_{n=0}^\infty \sum_{m=0}^n \binom{n}{m} \left( \frac{1}{2} \right)^m  $$ gilt
$$ \sum_{m=0}^n \binom{n}{m} \left( \frac{1}{2} \right)^m = \left( 1+\frac{1}{2}  \right)^n = \left( \frac{3}{2} \right)^n $$
Damit divergiert die Gesamtsumme, man kann aber nach der Formel für die geometrische Reihe den Wert von
$$ \sum_{n=0}^N \sum_{m=0}^n \binom{n}{m} \left( \frac{1}{2} \right)^m  $$ berechnen.

Comments

Hi ullim. Im Exponenten steht n+m.

Answer 2

Nach richtiger Anwendung von https://de.wikipedia.org/wiki/Binomischer_Lehrsatz

für die innere Summe ergibt sich (statt m hier die Laufvariable i):

Sum Binom(n,i)*(1/2)^{i+n},i=0...n

=pow(3/4,n) = (3/4)^n

was der Iterationsrechner online beweist:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm##@Ni=0;@N@Bi]=Iter(1,i,aD[0]=0,'i%3C=x','aD[0]+=Binom(x,i)/@P2,x+i);i++','aD[0]');@Ci]=@P3/4,i);@Ni%3E9@N0@N0@N#

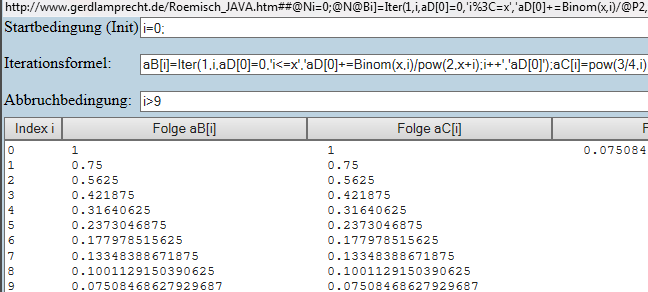
wobei die Funktion Iter(1,x,i, strSolangeWie, strUnterberechnung, strRückgabewert)

nichts weiter als die Untersumme ist, die in Array-Variable aB[i] abgelegt wird.

Nach Anwendung von https://de.wikipedia.org/wiki/Geometrische_Reihe

mit a[0]=1 ergibt sich der Gesamt-Grenzwert für beide Summen:

1/(1-3/4)= ... 

das kann man im Kopf :-)

Zugabe:

Erweiterung am Iterationsrechner:

Init-Zeile  noch zusätzlich aD[1]=0;

am Ende der Iterationsformel noch: aD[1]+=aB[i];

statt i>9 bis i>99 (oder 199) laufen lassen

und schon hat man das Gesamt-Ergebnis in aD[1]