Die Exponentialfunktion \(f(t) = Ce^{-at}\) genüge den Bedingungen \(f(0) = 2\) und \(f(1) = \frac{1}{2}\). Man bestimme die Konstanten C und α . Wie groß ist f(2)?
\(f(0) = Ce^{-a\cdot 0}= Ce^{-0}\)
\( Ce^{-0}=2\)
\( \frac{C}{e^{0}}=2\) mit \( e^{0}=1\):
\(C=\red{2}\):
\(f(1) = \red{2}e^{-a}\)
\( \red{2}e^{-a}=\frac{2}{e^{a}}\)
\(\frac{2}{e^{a}}=\frac{1}{2}\)
\(e^a=4\)
\(a\cdot \ln(e)=\ln(4)\) mit \(\ln(e)=1\):
\(a=\ln(4)\)
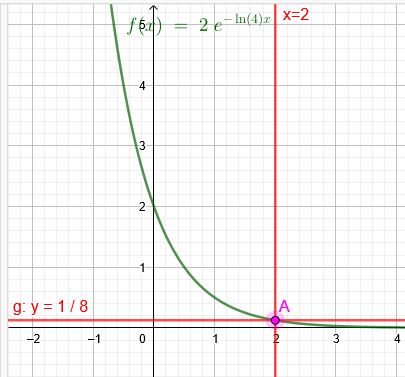
\(f(t) = 2e^{-\ln(4)t}\)
\(f(2) = 2e^{-\ln(4)\cdot 2}= 2e^{-\ln(4^2)}=2e^{-\ln(16)}=\frac{2}{e^{\ln(16)}}=\frac{2}{16}=\frac{1}{8}\)