ich habe gerade echt ein Problem. weil ich nicht weiter weiß-
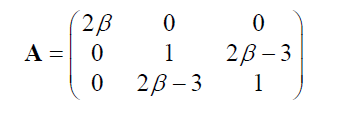
Eigenwerte von A
λ1 = 2β
λ2 = -2β +4
λ3 = 2β - 2
Ich habe die determinante der matrix gleich null gesetzt und komme dann auf drei nullstellen
β1= 0
β2= 1
β3= 2
für diese drei Werte β wäre die obige determinante = 0.
Jetzt möchte ich diese werte auf die anderen Kriterien prüfen.
Ich stelle fest dass zum Beispiel β1= 0 nicht geht.
Da es im widerspruch mit dem hauptminorekriterium steht, welches besagt erster hauptminor muss größer null sein.
da 2*0 = 0 ...... ist also genau null. Somit fällt β1 = 0 schon mal raus-.
anderes Beispiel mit dem Kriterium dass besagt alle Eigenwerte müssen größer oder gleich null sein.
setze ich nun "0" ein in λ3 so erhalte ich 2*0 - 2 = -2
-2 ist weder größer noch gleich null-.
Somit müsste doch die Matrix A für β1= 0 NICHT positiv semidefinit sein?
In der alten Lösung eines mitstudenten ist es aber als richtig gekennzeichnet.
Dort geltendie lösungen 0, 1, 2 als richtig