Wenn du das Verfahren quasi selbst erfinden darfst:
Hier mal, was eine orthogonale Projektion eines Vektors auf eine Gerade durch den Ursprung, ist:
Gegeben:
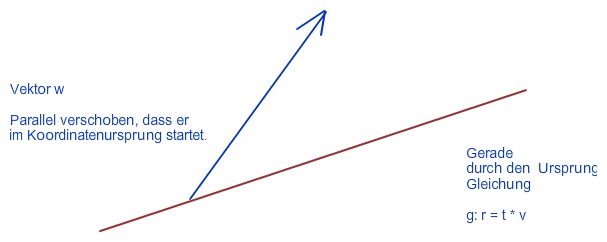
Konstruktion:
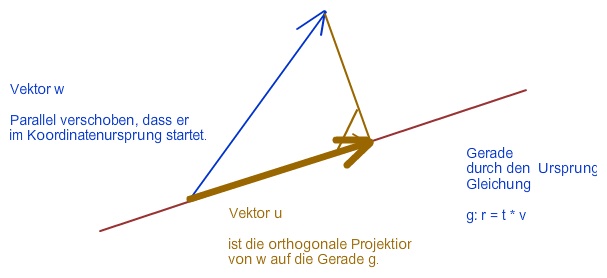
Illustration des Rechenwegs:
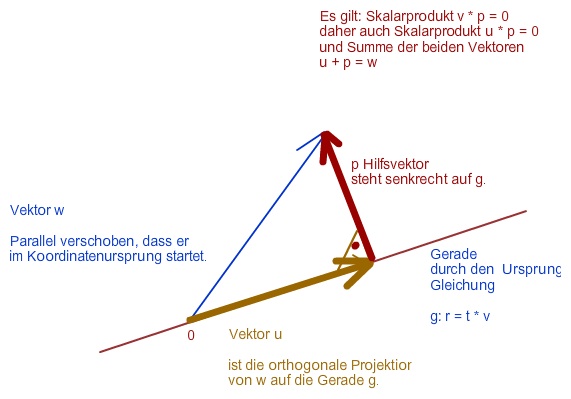
Nun das Ganze in höheren Dimensionen.
1. Schritt: Bestimme (Länge mal egal) p senkrecht auf v1, v2 und v3
Verwende Skalarprodukte v1*p = 0, v2*p=0 und v3*p = 0. Das sind 3 Gleichungen. Wähle die erste Koordinate daher beliebig. Z.B. als 1.
2. Schritt Gleichung aufstellen, die u enthält.
w = u + t * p , wobei u = a* v1 + b*v2 + c*v3
3. Schritt, einsetzen und die reellen Zahlen t, a,b,c bestimmen so, dass
w = a*v1 + b*v2 + c*v3 + t*p.
4. Schritt u ausrechnen.
Anmerkung: Gut möglich, dass das Ganze kürzer geht.