Kurvendiskussion 1.5. Flächenstück berechnen: Funktion lautet -(x^2)/(x+1), y= -x+1, y-Achse und x=u wobei u>0

Question

Aufgabe:

Gegeben ist für \( k \in R^{+} \) die Schar von Funktionen \( f_{k}: x \mapsto-\frac{x^{2}}{x+k} . \) Der Graph von \( f_{k} \) wird mit \( G_{k} \) bezeichnet.

1.1 Untersuche \( G_{k} \) auf Extrempunkte und Polstellen!

1.2 Bestimme die Kurve auf der die Extrempunkte aller Graphen \( G_{k} \) liegen.

1.3 Ermittle eine Gleichung der Schiefen Asymptote des Graphen \( G_{1}(\mathrm{k}=1) \) und zeige, dass diese den Graphen nicht schneidet.

1.4 Zeichne den Graphen \( G_{1} \) unter Verwendung aller bisherigen Ergebnisse zusammen mit seinen Asymptoten im Bereich \( -5<x<3 \). (Längeneinheit \( 1 \mathrm{~cm} \) ) Der Graph \( G_{1} \), die \( \mathrm{y}- \) Achse und die zwei Geraden mit den Gleichungen \( y=-x+1 \) sowie \( x=u \quad(u>0) \) schliessen ein Flächenstück vom Inhalt \( A(u) \) ein. Bestimme \( A(u) \) und berechne \( u \) so, dass \( A(u)=1 \) ist.

Wie löst man die Aufgabe 1.5?

Illustration aus dem Kommentar des Duplikats:

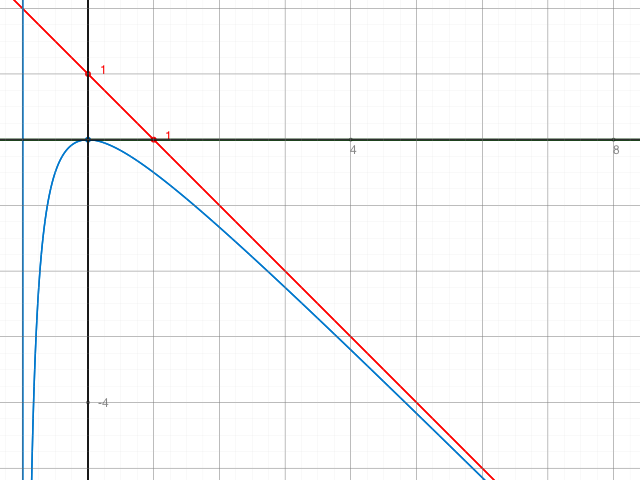
Also , die Funktion lautet  -(x²)/(x+1) (blau) , y= -x+1 (rot)  ,  und y=u wobei u>0.

Alle schliessen eine Fläche A(u) ein. Bestimme A(u) und berechne u so , dass A(u) = 1 ist.

Comments

Als Vorüberlegung: Finde den Schnittpunkt zwischen roter und blauer Linie. Das wird dann Deine rechte Grenze der Fläche sein. Mit y=u und der roten Funktion hast Du dann den zweiten, linken Schnittpunkt. Dabei ist u natürlich unbekannt, aber die Fläche als solches bekannt.

---

Hallo ausas,

  die Aufgabenstellung geht ja wie Kraut und Rüben durcheinander

 -(x²)/x+1 (blau) , y= -x+1 (rot)

  Wahrscheinlich heißt es :

  -(x^2)/(x+1). Dann dürfte die blaue Kurve stimmen.

  Wo ist u in der Skizze ? y = u ? Alle schließen eine Fläche ein.  ?

  Falls ich hieran weiterarbeiten soll dann zeichne die Skizze doch einmal richtig.

  mfg Georg

---

 

das ist sie .   x = u mit u>0 ...

---

Ich sehe keinen Sinn. es fehlt eine linke Grenze. Ist die y-Achse selbst eine Begrenzung?

---

ja für x = u ( u>0) bedeutet dass die Y achse begrenzt die Fläche ..

---

Eigentlich nicht^^. Das bedeutet nur, dass wir eine Fläche suchen, welche rechts der y-Achse endet.


Also nochmals zusammengefasst.

Wir suchen eine Fläche welche von der y-Achse, der Funktion y=-x^2/(x+1), der Funktion y=-x+1 und einer Senkrechten mit x=u (u>0) eingegrenzt ist und dabei den Wert 1 annimmt?

Answer 1

Hallo ,

f  = - x^2/( x+1)
g = -x + 1

x^2 : x + 1 = x - 1 + 1 / ( x + 1) Ι Polynomdivision

f = -x + 1 - 1 / ( x + 1 )

g - f= -x + 1 + x - 1 + 1 / ( x + 1 )
g - f = 1 / ( x + 1 )

∫ g - f= ln(x+1)

∫ g - f zwischen 0 und u

ln(u+1) = 1
ln(u + 1 ) = 1
u + 1 = e
u = e - 1
u = 1.71

mfg Georg

Bei Fehlern oder Fragen wieder melden